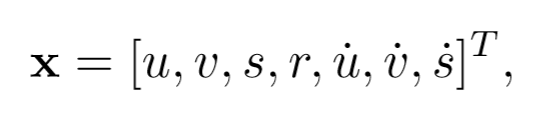SORT 톺아보기

SORT

• 실시간 객체 추적을 해줄수 있는 algorithm 입니다.
• GITHUB
• PAPER

논문을 읽어보고 코드 분석을 하겠습니다.

---

ABSTRACT

SORT는 실시간 추적을 위해 object들을 효과적으로 연관지어주는 것이 주 목적인 multi object tracking에 대한 실용적인 방법을 탐구하는 논문이다. detector 부분을 변경하는 것만으로도 tracking을 최대 18.9%까지 향상시킬 수 있다. Kalman Filter와 Hungarian algorithm과 같은 익숙한 기술을 기초로 하는 것만으로도 최신 online tracker에 필적하는 정확성을 제공한다. 또한 tracking하는 방식이 단순하기에 그에 따른 속도향상도 매우 높다.

• kalman filter 정리 -> HERE

---

INTRODUCTION

이 논문은 object가 각 frame에서 detection되고 bounding box로 표현되는 multiple object tracking(MOT) 문제에 대한 추적-탐지 프레임워크의 약식 구현을 제시한다.(YOLO에 적용하기 좋을 것 같다..). 다른 tracking 접근법과 달리 online tracking을 대상으로 한다. 그리고 실시간 추적을 효과적으로 하고 보행자 추적과 같은 애플리케이션의 성능 증진을 위한 효율성에 초점을 둔다. MOT문제는 video seqence의 여러 frame에서 detection을 연관시키는 것이 목적인 data association 문제로 볼수 있다. data association을 돕기 위해 tracker는 sequence의 object 및 appearance를 모델링하는 다양한 방법을 사용한다.

이 논문에서 사용된 방법은 최근에 확립 된 시각적 MOT benchmark를 관찰하며 동기를 부여받았다.

• 첫째, MHT(Multiple Hypothesis Tracking)과 JPDA(Joint Probabilistic Data Association)를 포함해 benchmark의 상위 순위를 차지하는 훌륭한 data association를 다시 등장시켰다.

• 둘째, ACF(Aggregate Channel Filter)를 사용하지 않은 tracker는 최상위 tracker이기 때문에 detection의 quality가 다른 detector를 방해할 수도 있다는 것을 나타낸다. 또한 accuracy와 speed 사이의 trade-off가 명확하게 나타난다.

• Occam's Razor 에 일치하도록, detection 구성요소를 벗어난 appearance은 tracking에서 무시되고, motion estimation과 data association에 모두 bounding box의 위치와 크기만 사용된다.

• 단기적, 장기적 occlusion에 관한 문제가 매우 드물게 발생하고 명시적인 치료로 인해 tracking framework에 바람직하지 않은 복잡성이 도입되므로 무시된다. object의 재증명 형태로 복잡성을 추가하면 tracking framework에 상당한 overhead가 추가되어서 실시간 detector에서의 사용이 제한될 수 있다고 주장한다.

• 이 설계는 다양한 edge cases 와 detection error를 처리하기 위해 다양한 구성요소를 통합 시킨 visual tracker들 과 대조적이다. 대신 공용 frame-to-frame 연관성에 효율적이고 믿을수 있는 처리에 초점을 맞춘다.

• detection errors에 대한 견고성을 목표로하기 보다는 visual object detection의 최근 발전을 이용하여 detection 문제를 직접 해결한다. 이는 보편적인 ACF 보행자 검출기와 CNN기반 검출기를 비교함으로써 입증된다.

• 추가적으로, 고전적이지만 매우 효율적인 두가지 방법인 Kalman filter,Hungarian method이 각각 tracking 문제의 움직임 예측과 데이터 연관요소를 처리하는데 사용된다. 이 논문에서의 접근법은 다양한 환경에서 human tracking에서만 사용하지만 다른 object에서도 가능하다.

---

LITERATURE REVIEW

전통적으로 MOT와 JPA를 사용해 해결했지만 불확실성이 높은 상태에서 어려운 결정을 지연시킨다. 그래서 객체 수가 기하급수적인 동적인 환경에서는 실시간 응용 프로그램에 비실용적이다.

Rezatofighi et al

최근에 Rezatofighi et al는 integer programs의 문제를 해결할 때 최근 발전을 이용해 JPDA의 효율적인 근사치를 통해 combinatorial complexity 문제를 해결하기 위한 목적으로 MOT에서 JPDA공식을 재 검토했다.

Kim et al

유사하게 Kim et al은 최첨단 성능을 달성하기 위해 각 타겟에 대한 appearance models을 사용해 MHT그래프를 잘랐다. 그러나 이러한 방법으로는 의사결정이 지연되기 때문에 online tracking에 적합하지 않다.

Geiger et al

Geiger et al에 의한 방법은 2단계 처리에 Hungarian algorithm을 사용한다. 첫번째로 인접한 frame에 detection을 연결해서 geometry와 appearance cues가 결합되어 tracklets을 형성되고 여기에서 geometry와 appearance cues가 결합되어서 유사도행렬을 형성한다. 그런 다음 tracklets는 서로 연결되어 occlusion으로 인해 궤적을 깨뜨리고 다시 geometry와 appearance cues를 사용한다.

---

METHODOLOGY

이 논문에서 제안한 방법은

• detection의 주요 구성요소
• object의 상태를 미래의 frame에게 전달
• 현재 detection을 기존 object와 연결하고 tracking된 object 상태

를 관리하면서 설명된다.

Detection

• FrRCNN(Faster Region CNN)을 사용한다. FrRCNN은 end-to-end framework이며 첫번째 단계에서 feature를 추출하고 propose region에서 두번째 단계를 위해서 object를 classification하는 영역을 제안한다.

• PASCAL VOC를 학습시켰고 보행자만 detection하고 output accuracy가 50%를 초과하는 결과만 전달한다.

• FrRCNN과 ACF를 비교하고 detection quality가 tracking 성능에 중요한 역할을 한다고 깨달았다.

Estimation Model

• 다른 object와 카메라의 motion 과는 무관한 linear constant velocity model을 사용하여 각 object의 frame간의 변위에 대해 설명한다.

• u : target의 중심 가로 픽셀 위치
• v : target의 중심 세로 픽셀 위치
• s : target의 bounding box의 크기
• r : target의 bounding box의 종횡비(가로 : 세로 비율)

• T :

• detection이 target과 연관이 있을 때, 검출된 bounding box는 target의 상태를 업데이트 하는데 사용되고, 여기서 속도 성분은 Kalman Filter를 통해 최적화한다.

• detection이 target과 연관이 없을 때 그 상태는 단순히 예측된다.

Data Association

• 기존 target을 detection하는 경우 각 target의 bounding box의 geometry 정보는 현재 frame에서 새로운 위치를 예측해 추정된다.

• 그 assignment cost matrix은 기존 target으로 부터 모든 bounding box를 예측하고 IOU거리로 계산한다. assignment는 Hungarian algorithm을 사용해 해결한다. 또한 최소 IOU는 target의 겹침이 IOUmin 보다 작은 할당을 거부하는데 적용된다.

• bounding box의 IOU 거리는 암묵적으로 대상을 지나가면서 발생하는 단기간의 occlusion을 처리한다. IOU거리는 유사한 척도의 검출을 적절하게 선호하기 때문에 occlusion을 잘 처리할수 있다.

궁금하다.. 나중에 코드를 통해 자세히 알아보자

Creation and Deletion of Track Identities

• object가 이미지를 input하거나 이미지를 떠날 때 고유한 ID를 생성하거나 제거해야한다.

• tracker를 생성하기 위해서 tracking되지 않은 object의 존재를 나타내기 위해 IOUmin보다 작은 중복을 가진 모든 탐지를 고려한다.

• tracker는 0으로 설정된 속도로 bounding box의 geometry을 사용해 초기화 된다. 이 시점에서는 속도가 관측되지 않으므로 공분산은 불확실성에 의해서 큰 값으로 초기화한다.

• 새로운 tracker는 target이 없는데 있다고하는 오류를 방지하기 위한 충분한 증거를 축적해야 한는 시험 기간을 거친다. track은 TLost frame에 대해 detection되지 않으면 종료한다.

모든 실험에서 TLost는 두가지 이유로 1로 설정된다.

• 첫쨰, 등속 모델은 실제 동적인 예측이 좋지 않다.

• 두번쨰, object 재식별이 작업의 범위를 벗어나는 frame-to-frame tracking과 관련있다. 또한 손실된 target을 초기에 삭제하면 효율이 높다.

TLost가 정확히 뭔지 몰라서 코드를 살펴보며 알아봐야할것 같다

---

결론

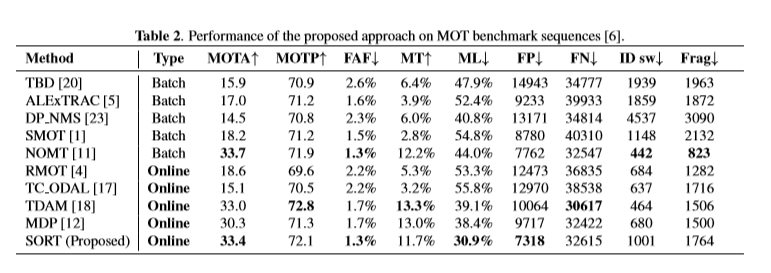
• MOTA(↑): Multi-object tracking accuracy.

• MOTP(↑): Multi-object tracking precision.

• FAF(↓): number of false alarms per frame.

• MT(↑): number of mostly tracked trajectories. I.e. target has the same label for at least 80% of its life span.

• ML(↓): number of mostly lost trajectories. i.e. target is not tracked for at least 20% of its life span.

• FP(↓): number of false detections.

• FN(↓): number of missed detections.

• ID sw(↓): number of times an ID switches to a different previously tracked object.

• Frag(↓): number of fragmentations where a track is interrupted by miss detection.

---

코드 까보기

함수별로 간단하게 한번 알아보고 아까 궁금했던것들 위주로 보겠습니다.

IOU

@jit
def iou(bb_test,bb_gt):
  """
  [x1,y1,x2,y2] 형태의 박스 2개 비교
  """
  xx1 = np.maximum(bb_test[0], bb_gt[0])
  yy1 = np.maximum(bb_test[1], bb_gt[1])
  xx2 = np.minimum(bb_test[2], bb_gt[2])
  yy2 = np.minimum(bb_test[3], bb_gt[3])
  w = np.maximum(0., xx2 - xx1)
  h = np.maximum(0., yy2 - yy1)
  wh = w * h
  o = wh / ((bb_test[2]-bb_test[0])*(bb_test[3]-bb_test[1])
    + (bb_gt[2]-bb_gt[0])*(bb_gt[3]-bb_gt[1]) - wh)
  return(o)

iou(bounding box의 겹칩)를 구하는 함수

convert_bbox_to_x

def convert_bbox_to_z(bbox):
  w = bbox[2]-bbox[0]
  h = bbox[3]-bbox[1]
  x = bbox[0]+w/2.
  y = bbox[1]+h/2.
  s = w*h    #scale is just area
  r = w/float(h)
  return np.array([x,y,s,r]).reshape((4,1))

위에 estimate model에서 식을 구현하였다. [x1,y1,x2,y2] -> [x,y,s,r]

• u : target의 중심 가로 픽셀 위치
• v : target의 중심 세로 픽셀 위치
• s : target의 bounding box의 크기
• r : target의 bounding box의 종횡비(가로 : 세로 비율)

convert_x_to_bbox

def convert_x_to_bbox(x,score=None):
  w = np.sqrt(x[2]*x[3])
  h = x[2]/w
  if(score==None):
    return np.array([x[0]-w/2.,x[1]-h/2.,x[0]+w/2.,x[1]+h/2.]).reshape((1,4))
  else:
    return np.array([x[0]-w/2.,x[1]-h/2.,x[0]+w/2.,x[1]+h/2.,score]).reshape((1,5))

위에 함수와 반대로 [x,y,s,r] -> [x1,y1,x2,y2]

KalmanFilter

from filterpy.kalman import KalmanFilter

class KalmanBoxTracker(object):
  """
  이 class는 bounding box로 tracking object의 내부 상태를 나타낸다.
  """
  count = 0
  def __init__(self,bbox):
    """
    bounding box를 이용해 tracker 초기화
    """
    # 등속모델 정의
    # dim_x : 상태 변수의 수
    # dim_z : 측정 입력의 수(좌표의 수) [x1,y1,x2,y2] = 4
    self.kf = KalmanFilter(dim_x=7, dim_z=4)

    # 상태전이행렬
    self.kf.F = np.array([[1,0,0,0,1,0,0],[0,1,0,0,0,1,0],[0,0,1,0,0,0,1],[0,0,0,1,0,0,0],[0,0,0,0,1,0,0],[0,0,0,0,0,1,0],[0,0,0,0,0,0,1]])
    # 측정 기능
    self.kf.H = np.array([[1,0,0,0,0,0,0],[0,1,0,0,0,0,0],[0,0,1,0,0,0,0],[0,0,0,1,0,0,0]])

    # 측정 잡음행렬
    self.kf.R[2:,2:] *= 10.
    # 공분산 행렬
    self.kf.P[4:,4:] *= 1000.
    self.kf.P *= 10.
    # 프로세스 잡음행렬
    self.kf.Q[-1,-1] *= 0.01
    self.kf.Q[4:,4:] *= 0.01

    # 상태 측정 벡터
    self.kf.x[:4] = convert_bbox_to_z(bbox)
    self.time_since_update = 0
    self.id = KalmanBoxTracker.count
    KalmanBoxTracker.count += 1
    self.history = []
    self.hits = 0
    self.hit_streak = 0
    self.age = 0

  def update(self,bbox):
    """
    상태 업데이트(재귀적)
    """
    self.time_since_update = 0
    self.history = []
    self.hits += 1
    self.hit_streak += 1
    self.kf.update(convert_bbox_to_z(bbox))

  def predict(self):
    """
    벡터상태수정 and 예측된 bounding box 추정치 반환.(재귀적)
    """
    if((self.kf.x[6]+self.kf.x[2])<=0):
      self.kf.x[6] *= 0.0
    self.kf.predict()
    self.age += 1
    if(self.time_since_update>0):
      self.hit_streak = 0
    self.time_since_update += 1
    self.history.append(convert_x_to_bbox(self.kf.x))
    return self.history[-1]

  def get_state(self):
    """
    현재 bounding box 추정치 반환
    """
    return convert_x_to_bbox(self.kf.x)

associate_detections_to_trackers

from sklearn.utils.linear_assignment_ import linear_assignment

def associate_detections_to_trackers(detections,trackers,iou_threshold = 0.3):
  """
  tracking object(둘 다 bounding box)에 detection을 지정합니다.
  unmatched_detections 및 unmatched_trackers와 match 3 개의 목록을 반환합니다.
  """

  # 추적 하는게 없다면 반환
  if(len(trackers)==0):
    return np.empty((0,2),dtype=int), np.arange(len(detections)), np.empty((0,5),dtype=int)
  iou_matrix = np.zeros((len(detections),len(trackers)),dtype=np.float32)


  for d,det in enumerate(detections):
    for t,trk in enumerate(trackers):
      iou_matrix[d,t] = iou(det,trk)
  #Hungarian Algorithm
  matched_indices = linear_assignment(-iou_matrix)

  unmatched_detections = []
  for d,det in enumerate(detections):
    if(d not in matched_indices[:,0]):
      unmatched_detections.append(d)
  unmatched_trackers = []
  for t,trk in enumerate(trackers):
    if(t not in matched_indices[:,1]):
      unmatched_trackers.append(t)

  #낮은 IOU와 일치하는 filter
  matches = []
  for m in matched_indices:
    if(iou_matrix[m[0],m[1]]<iou_threshold):
      unmatched_detections.append(m[0])
      unmatched_trackers.append(m[1])
    else:
      matches.append(m.reshape(1,2))
  if(len(matches)==0):
    matches = np.empty((0,2),dtype=int)
  else:
    matches = np.concatenate(matches,axis=0)

  return matches, np.array(unmatched_detections), np.array(unmatched_trackers)

Sort

class Sort(object):
  def __init__(self,max_age=1,min_hits=3):
    self.max_age = max_age
    self.min_hits = min_hits
    self.trackers = []
    self.frame_count = 0

  def update(self,dets):
    """
    Params:
      dets - [[x1,y1,x2,y2,score],[x1,y1,x2,y2,score],...]
    요구 사항 : 빈 frame이있는 경우에도 각 frame마다 한 번 호출해야합니다.
    마지막 열이 object ID 인 유사도 배열을 반환합니다.
    NOTE: 반환 된 object 수는 제공된 detection 수와 다를 수 있습니다.
    """
    self.frame_count += 1
    #existing trackers로 부터 예상위치를 얻는다
    trks = np.zeros((len(self.trackers),5))
    to_del = []
    ret = []
    for t,trk in enumerate(trks):
      pos = self.trackers[t].predict()[0]
      trk[:] = [pos[0], pos[1], pos[2], pos[3], 0]
      if(np.any(np.isnan(pos))):
        to_del.append(t)
    trks = np.ma.compress_rows(np.ma.masked_invalid(trks))
    for t in reversed(to_del):
      self.trackers.pop(t)
    matched, unmatched_dets, unmatched_trks = associate_detections_to_trackers(dets,trks)

    #지정된 detection이 있는 tracker 업데이트
    for t,trk in enumerate(self.trackers):
      if(t not in unmatched_trks):
        d = matched[np.where(matched[:,1]==t)[0],0]
        trk.update(dets[d,:][0])

    #unmatched detections을 위한 새로운 tracker 생성/초기화
    for i in unmatched_dets:
        trk = KalmanBoxTracker(dets[i,:])
        self.trackers.append(trk)
    i = len(self.trackers)
    for trk in reversed(self.trackers):
        d = trk.get_state()[0]
        if((trk.time_since_update < 1) and (trk.hit_streak >= self.min_hits or self.frame_count <= self.min_hits)):
          ret.append(np.concatenate((d,[trk.id+1])).reshape(1,-1)) # +1 as MOT benchmark requires positive
        i -= 1
        #dead tracklet 제거
        if(trk.time_since_update > self.max_age):
          self.trackers.pop(i)
    if(len(ret)>0):
      return np.concatenate(ret)
    return np.empty((0,5))

---

용어

• Occam's Razor : 절감의 법칙(어떤 현상을 설명하는 데는 가장 단순한 가설로 시작해야하고 가설을 필요 이상으로 정립하지 말라는 것)

• occlusion : object를 추적하는 시스템을 개발하는 경우, 추적중인 object가 다른 object에 숨겨진 경우를 뜻한다.

• tracklets : 단편적 궤적

• 유사도행렬 : 유사도가 높을수록 최대한 높은 값을 가지게하고 유사도가 낮을수록 최대한 0에 가깝게 값을 만든다. clustering

• linear constant velocity : 선형 등속 모델

Hungarian algorithm

할당문제(assignment problem)를 해결하기 위한 알고리즘이고 할당문제란 n명의 사람에게 중복없이 일을 부여하고 총 할당 비용을 최소로 하는 해를 구하는 것이라고 정의할 수 있다.

1. 각 할당되는데 발생하는 비용을 비용행렬로 만들어서 각 행과 열에서 최소값을 제거한다.

2. 최소의 라인으로 0의 성분을 가진 행과 열을 지운다.

3. 지워지지 않는 성분 중 최소값을 찾아 이를 지워지지 않는 성분에서 빼고 각 라인이 겹치는 성분에서는 더한다.

4. 각 열과 행에 0이 하나씩 있도록 0의 성분을 찾는다.

---

참조

• https://github.com/abewley/sort
• https://arxiv.org/abs/1602.00763