Kalman Filter 톺아보기
Kalman Filter
kalman filter는 과거의 정보와 새로운 측정값을 사용하여 측정값에 포함된 Noise를 제거시켜 추정하는 최우선 추정 알고리즘 이고an optimal recursive data processing algorithm이라고 불린다.학생이 한명씩 점수를 말하면 그때마다 평균을 짐작해보자
1
2
3
4
5
6
7
X'(1) = X1
X'(2) = (X1 + X2) / 2 = (X'(1)*1 + X2) / 2
X'(3) = (X1 + X2 + X3) / 3 = (X'(2)*2 + X3) / 3
'
'
'
X'(n) = (X1 + X2 + .... + Xn) / n = (X'(n-1)*(n-1) + Xn) / n
위에 식을 아래로 변환
1
X'(n) = X'(n-1) * ((n-1)/n) + (1/n) * Xn
- 즉, 끝에 두개의 값만 있으면 평균을 구할 수 있다. 결론은 선형적 움직임을 갖는 대상을 재귀적으로 동작시키는 것이다.
종류
LKF : Linear Kalman Filter
EKF : Extended Kalman Filter, 선형성 가정을 완화시켜 확장시킨 버전, 최적의 수행은 아니고 초기 추정이 틀릴경우 발산할 수 있음
UKF : the Unscented Kalman Filter, 상태 천이와 관찰모델이 매우 비선형일 경우 사용됨
중요도
- 만약에 입력이 2개일때 2개 각각에는 어느것이 더 중요하다고 생각되는 중요도의 개념이 적용되어야한다. 그렇기 떄문에 평균에서 얼마나 더 벗어났는지에 대한 지표인
표준편차의 제곱에 반비례 한다. 즉, 표준편자가 클수록 그 값이 평균에서 멀어진다는 뜻이기 때문에 중요도는 작아질 것이다.
1
평균 = X1 * (표준편차2)^2 + X2 * (표준편차1)^2 / ((표준편차1)^2 + (표준편차2)^2)
공분산
각 확률변수들이 어떻게 퍼져있는지를 나타내는 것
두변수 간의 변동성(관계)
1
2
3
4
5
Cov(X, Y) > 0 X가 증가 할 때 Y도 증가한다.
Cov(X, Y) < 0 X가 증가 할 때 Y는 감소한다.
Cov(X, Y) = 0 공분산이 0이라면 두 변수간에는 아무런 선형관계가 없으며 두 변수는 서로 독립적인 관계에 있음을 알 수 있다
전이 행렬
- 상태가 전이 될 확률 상태1을 x라고 하고 상태2를 y라고 할 때
1
2
3
4
x -> x
x -> y
y -> y
y -> x
위에 네가지 경우 처럼 어떤 상태에서 어떤 상태로 가는데 나오는 확률을 행렬로 나타낸 것이다.
- 모든 원소의 값이 0보다 크거나 같다.
- column의 원소의 합은 1이 된다.
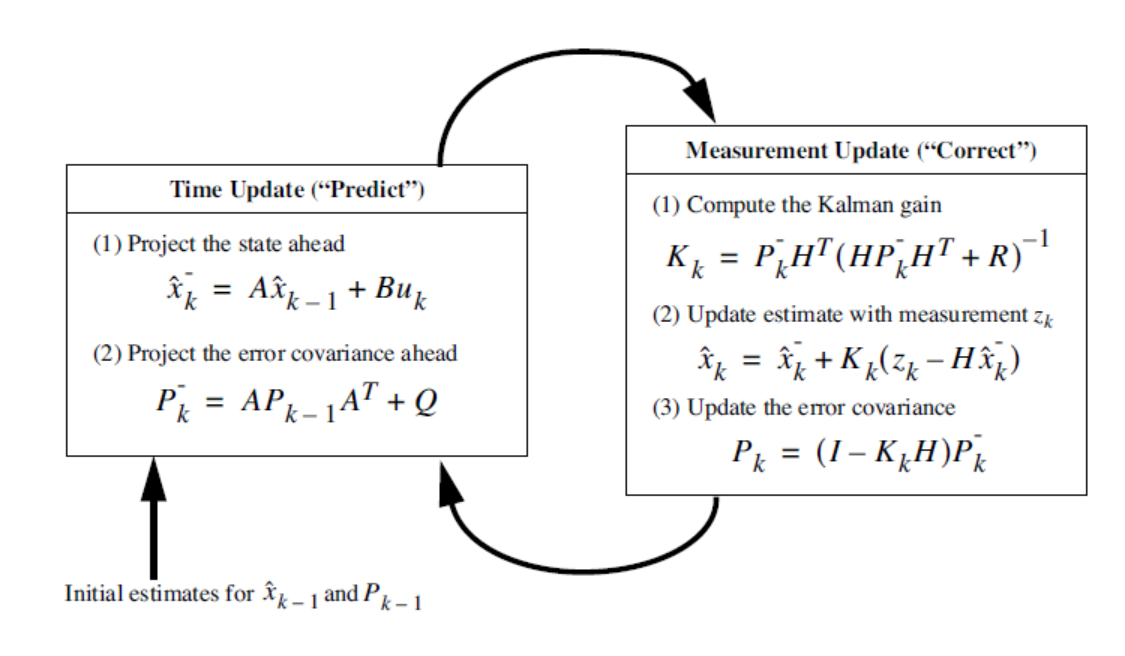
공식정리
A,B,H: 이전 상태 전이 행렬(시스템에 따라 결정되는 값으로 변하지 않음)A: (n*n) 행렬B: (n*l) 행렬H: (m*n) 행렬k: 시간x: 시스템의 상태zk: 센서를 이용한 측정값w: 시스템 잡음v: 측정 잡음K: kalman 이득P: 오차 공분산 행렬Q: 시스템 잡음(Buk)R: 측정 잡음의 공분산 행렬^: estimate-: 아직 고쳐지지 않았다.(이전의 값)
Time Update
과거 데이터를 토대로 현재값을 예측하는 부분
) 현재값을 예측
) 오차 공분산을 예측
Measurement Update
새로운 측정값으로 올바르게 고쳐주는 부분
- ) kalman 이득을 구한다.
- 측정 잡음(R)이 클수록 이득이 적어지고 작을수록 커진다.
) 올바르게 고쳐진 상태변수 갱신
- ) 올바르게 고쳐진 공분산 갱신
정리
위에 내용들을 종합해 보면 측정 잡음을 포함하는 입력을 노이즈가 제거된 정확한값으로 다음 상태를 확률적으로 추정하는 알고리즘입니다. kalman filter는 상태 예측(state prediction)과 측정 업데이트(measurement update)를 재귀적 으로 현재상태를 계산한다. 상태 예측에서는 이전 상태의 값의 확률분포와 입력의 확률분포를 통해 현재 값을 예측하고, 측정 업데이트는 상태 예측단계에서 예측한 현재 값 그리고 실제 현재 값을 이용해 값을 갱신하는 알고리즘이다.