선형대수학 끄적이기
가끔 기억 안날때 보려고 한줄식으로 매우 간략하게 적었다. 자세한 내용을 알고 싶으시면 [Here] 이 곳 수업에서 알아보시는 것을 추천한다.
기하학적인 정의는 Here 유튜브에 알기 쉽게 나와 있었다.
벡터
- vector = 크기 + 방향
- 순서가 정해져 있다.
- one-dimension
- lowercase
- 표현 : \(x = [1,2,3] \in \mathbb{R}^3\) (3차원 벡터)
행렬
- row vector, column vertor
- 행렬곱 : \(AB \neq BA\)
- uppercase
정방행렬
\[\begin{pmatrix} x_{11} & \cdots & x_{1n} \\ \vdots & \ddots & \vdots \\ x_{n1} & \cdots & x_{nn} \end{pmatrix}\]- 행과 열의 길이가 같은 정사각 행렬
항등 행렬(Identity Matrix)
\[\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\]- 가운데 값이 1이고 나머지가 0
- 어떤 행렬과 곱해져도 그 행렬이 나온다.
- 행렬 x 역행렬 = 항등행렬
- 직사각행렬은 안된다.
전치행렬
\[\begin{pmatrix} x_{11} & x_{12} & x_{13} \\ x_{21} & x_{22} & x_{23} \end{pmatrix} \Rightarrow \begin{pmatrix} x_{11} & x_{21} \\ x_{12} & x_{22} \\ x_{13} & x_{23} \end{pmatrix}\]- transpose matrix
대각행렬
\[diag(x_1, x_2, x_3) = \begin{pmatrix} x_1 & 0 & 0 \\ 0 & x_2 & 0 \\ 0 & 0 & x_3 \end{pmatrix}\]- diagonal matrix
대각합(trace)
\[X = \begin{pmatrix} x_1 & 0 & 0 \\ 0 & x_2 & 0 \\ 0 & 0 & x_3 \end{pmatrix}\] \[Tr(X) = x_1 + x_2 +x_3\]linear equation
\[a_1 x_1 + a_2 x_2 + \cdots + a_n x_n = b\]\(a^T x = b\) 위에 식과 같은식인데 transpose를 해주는 이유는 shape을 맞추기 위함
- \(a\) : 계수(coefficient)
linear combination
span : 벡터 v1, v2의 선형 조합으로 만들어지는 space
재료 벡터 \(a_1, a_2, a_3\)의 span안에 b가 존재한다면 값이 존재한다.
\[\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}\begin{bmatrix} 1 & 2 & 3 \end{bmatrix} = \begin{bmatrix} 1 & 2 & 3 \\ 1 & 2 & 3 \\ 1 & 2 & 3 \end{bmatrix}\]
반대로 진행하면??
\[\begin{bmatrix} 1 & 2 & 3 \\ 1 & 2 & 3 \\ 1 & 2 & 3 \end{bmatrix} = \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}\begin{bmatrix} 1 & 2 & 3 \end{bmatrix}\]만약 3x3 matrix가 일정한 값이 아니라면 위와 같이 분해하는건 불가능하다. 하지만 근사하게는 만들어 줄 수 있을 것이다.
선형 독립 / 선형 종속
- linearly independent, linearly dependent
이 경우 x1, x2, x3가 나오는 경우의 수는 셋다 0인 경우의 수 밖에 없다. 그렇다면 이것이 선형 독립(linearly independent)
\[\begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix} x_1 + \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} x_2 + \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} x_3 = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}\]이 경우 x1, x2, x3가 나오는 경우의 수 무수히 많다. 그렇다면 이것이 선형 종속(linearly dependent)
Basis
- 벡터공간의 축들을 만들 수 있는 벡터들의 집합
- 공간을 구성하는 벡터
- 벡터의 집합이 linearly independent하고 그 벡터의 집합이 전체 벡터의 space를 span하는 것이 basis다.
벡터의 집합 \(\left \{ (1,0,0),(0,1,0),(0,0,1) \right \}\)은 \(\mathbb{R}^3\)의 \(basis\)다.
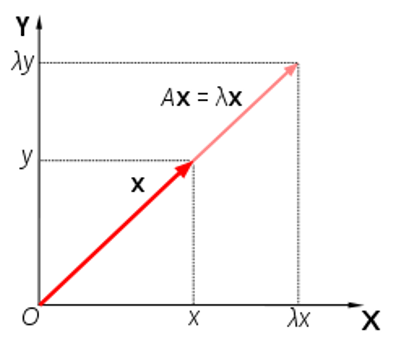
고유값 / 고유벡터
- eigenvalue, eigenvector
선형 변환(\(A\))을 할 때 크기만 변하고 방향이 변하지 않는 벡터
\[Ax = \lambda x\]여기서 \(\lambda\)가 eigenvalue, \(x\)는 eigenvector다.
Orthogonal / Orthonormal
Orthogonal
- 기호 : \(\perp\)
- 직교하다.
- 직교하기 때문에 선형독립이다.
- 두 벡터의 내적이 0이다.
Orthonormal
- Orthogonal하다.
- 길이가 1인 벡터로 이루어져 있다.
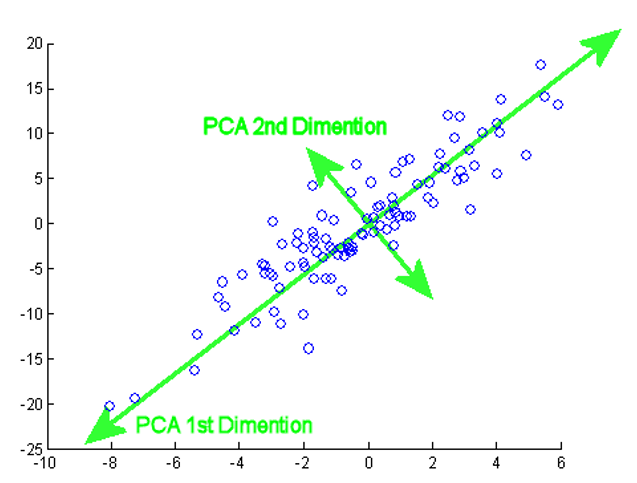
PCA(Principal Component Analysis)
- 주성분 분석
- 차원 축소(dimensionality reduction), 변수 추출(feature extraction)
- 공분산 행렬의 eigenvector
- 데이터의 구조를 잘 살려주면서 dimension reduction하는 방법
데이터의 variance를 최대한 보존하면서 서로 orthgonal하는 새로운 basis를 찾아, high dimension space의 표본들을 선형 연관성이 없는 low dimension으로 변환하는 방법
- 2차원 벡터를 1차원 벡터로 축소시키는 최적의 방법은 variance를 최대로 만들어주는 eigenvector에 정사영 시키는 것
순서
- 공분산 행렬을 구한다.
- 공분산 행렬을 eigendecomposition 한다.
- eigenvalue가 큰 순서대로 정렬한다.
- 관심이 있는 dimension까지만 사용하고 \(X\)와 eigenvector를 내적한다.
공분산 행렬
feature들의 상관관계의 정도(커지면 작아지고, 작아지면 커지고, 커지면 커지고, 작아지면 작아지는 정도)
상관관계를 알기 위해서 각 feature를 내적해서 유사성을 찾는다.
내적의 기하학적 의미
\[A \cdot B = \left | A \right | \left | B \right | \cos \theta\]- 각도에 따라서 A와 B가 얼마나 유사 한지 알 수 있다. 각도가 90도라면 연관성이 없고 0도라면 방향이 같기 때문에 유사하다는 것을 알 수 있다.
순서
- 각 행 별로 평균을 구한 뒤 빼준다.
- 내적하고 \(X\)의 수만큼 나누어준다.
- 행렬의 대각은 분산식이 되고 나머지는 공분산식이 된다.
- 공분산 행렬 완성
고유값 분해(eigendecomposition)
- 주어진 데이터 \(A\)
- \(det(A - \lambda I) = 0\)를 만족하는 \(\lambda\)를 찾는다.
- \(\lambda\)를 대입하여 고유벡터행렬 \(V\)를 찾는다.
- \(A = VDV^{-1}\)로 부터 대각화 행렬을 얻어야한다. (\(D = V^{-1}AV\))
고윳값 분해를 이용하는 것은 A가 정사각 행렬일 경우만 가능한 방법이다. 직사각행렬일때는 어떻게 해야하나?? 그때 나오는게 특이값 분해(SVD)가 있다. 특이값 분해는 생략한다.
LDA(Linear Discriminant analysis)
- dimension 축소가 아닌 dimension 분리의 목적
- 각 클래스의 집단 내부의 분산은 작다.
- 서로 다른 클래스 사이의 분산은 커야한다.
Fisher linear discriminant
Fisher가 제안한 linear discriminant의 목적함수
\[S_i = \sum_{s \in w_i} (X - m_i)(X - m_i)^T\] \[S_1 + S_2 = S_w\] \[J(w) = \frac{\left | m_1 - m_2 \right |}{S_1^2 + S_2^2} = \frac{w^T S_b^{LDA}w}{w^T S_w^{LDA}w}\]분자는 최대화시켜야하고 분모를 최소화 시키는 값을 찾아야한다. 그러기 위해서는 \(w\)에 대해서 미분한 값이 0이 되는(수평)값을 찾아야한다. 아래 식이 \(J(w)\)를 미분해 0이 나오는 식을 풀어낸 것이다.
\[S^{-1}_w S_b w = \lambda w\]식을 풀어내는 방식은 이 곳을 참조해서 보는 것을 추천한다.
순서
- 전체, 각 클래스의 평균을 계산한다.
- 서로 다른 클래스 사이의 분산을 계산한다.
- 각 클래스 내부의 분산을 계산한다.
- eigendecomposition을 한다.
- 관심이 있는 dimension까지만 사용하고 \(X\)와 eigenvector를 내적한다.