Deep Learning Interviews 끄적이기

Posted Jan 12, 2022 Updated Feb 21, 2024

By Jaemin Jeong

34 min read

Deep Learning Interviews 정리

딥러닝의 기초를 생각날때 마다 공부해주기
현재 저자분이 계속 업데이트 중 -> Here

Kindergarten

LOGISTIC REGRESSION

General Concepts

Question

True or False: For a fixed number of observations in a data set, introducing more variables normally generates a model that has a better fit to the data. What may be the drawback of such a model fitting strategy?

Answer

True

However, when an excessive and unnecessary number of variables is used in a logistic regression model, peculiarties of the underlying data set disproportionately affect the coefficients in the model, a phenomena commonly referred to as “overfitting”. Therefore, it is important that a logistic regression model does not start training with more variables than is justified for the given number of observations.

Question

Define the term “odds of success” both qualitatively and formally. Give a numerical example that stresses the relation between probability and odds of an event ocurring.

Answer

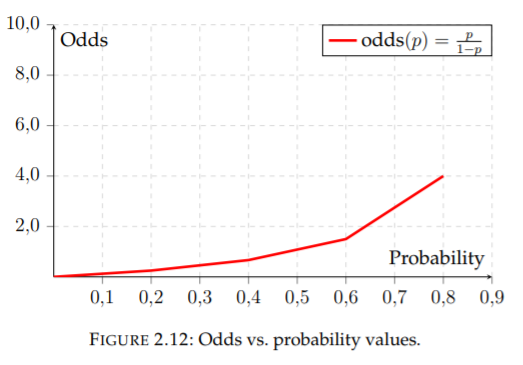
The odds of success are defined as the ratio between the probability of success $p \in [ 0, 1 ]$ and the probability of failure $1 - p$. Formally:

\[Odds(p) = ( \frac{p}{1-p} )\]

Question

Define what is meant by the term “interaction”, in the context of a logistic regression predictor variable.
What is the simplest form of an interaction? Write its formulae.
What statistical tests can be used to attest the significance of an interaction term?

Answer

An interaction is the product of two single predictor variables implying a non-additive effect
The simplest interaction model includes a predictor variable formed by multiplying two ordinary predictors. Let us assume two variables X and Z. Then, the logistic regression model that employs the simplest form of interaction follows:

\[\beta_0 + \beta_1 X + \beta_2 Z + \beta_3 X Z\]

where the coefficient for the interaction term $XZ$ is represented by predictor $\beta_3$.

For testing the contribution of an interaction, two principal methods are commonly employed; the Wald chi-squared test or a likelihood ratio test between the model with and without the interaction term. Note: How does interaction relates to information theory? What added value does it employ to enhance model performance?

Wale chi-squared : $x^2 = \sum ( O - E )^2 / E$

O는 관측값

E는 기댓값

독립성 검정에 사용하며 이는 서로 독립적인지 아닌지를 검증

값이 클수록 중요한 feature -> p-value와 반비례

Question

True or False: In machine learning terminology, unsupervised learning refers to the mapping of input covariates to a target response variable that is attempted at being predicted when the labels are known.

Answer

False

This is exactly the definition of supervised learning; when labels are known then supervision guides the learning process.

response variable : Y로 표기 되며 지도학습으로 예측되는 변수

Question

Compute the following sentence: In the case of logistic regression, the response variable is the log of the odds of being classified in […].

Answer

In the case of logistic regression, the response variable is the log of the odds of being classified in a group of binary or multi-class responses. This definition essentially demonstrates that odds can take the form of a vector.

Question

Describe how in a logistic regression model, a transformation to the response variable is applied to yield a probability distribution. Why is it considered a more informative representation of the response?

Answer

When a transformation to the response variable is applied, it yields a probability distribution over the output classes, which is bounded between 0 and 1; this transformation can be employed in several ways, e.g., a softmax layer, the sigmoid function or classic normalization. This representation facilitates a soft-decision by the logistic regression model, which permits construction of probability-based processes over the predictions of the model. Note: What are the pros and cons of each of the three aforementioned transformations?

Question

Complete the following sentence: Minimizing the negative log likelihood also means maximizing the […] of selecting the […] class.

Answer

Minimizing the negative log likelihood also means maximizing the likelihood of selecting the correct class.

Odds, Log-odds

Question

Assume the probability of an event occurring is $p = 0.1$.

What are the odds of the event occurring?
What are the log-odds of the event occurring?
Construct the probability of the event as a ratio that equals 0.1.

Answer

\[odds = \frac{0.1}{0.9}\]
\[log-odds = ln(0.1 / 0.9) = -2.19685\]
\[probability = \frac{odds}{odds + 1} = \frac{0.11}{1.11} = 0.1\]

Question

True or False: If the odds of success in a binary response is 4, the corresponding probability of success is 0.8.

Answer

True

\[odds = \frac{0.8}{0.2} = 4\]

Question

Draw a graph of odds to probabilities, mapping the entire range of probabilities to their respective odds.

Answer

Question

The logistic regression model is a subset of a broader range of machine learning models known as generalized linear models (GLMs), which also include analysis of variance (ANOVA), vanilla linear regression, etc. There are three components to a GLM; identify these three components for binary logistic regression.

Answer

A binary logistic regression GLM consists of there components:

Random component: refers to the probability distribution of the response variable (Y ), e.g., binomial distribution for Y in the binary logistic regression, which takes on the values Y = 0 or Y = 1.
Systematic component: describes the explanatory variables: (X1, X2, …) as a combination of linear predictors. The binary case does not constrain these variables to any degree.
Link function: specifies the link between random and systematic components. It says how the expected value of the response relates to the linear predictor of explanatory variables.

Question

Let us consider the logit transformation, i.e., log-odds. Assume a scenario in which the logit forms the linear decision boundary:

\[log (\frac{Pr(Y = 1 | X)}{Pr(Y = 0 | X)}) = \theta_0 + \theta^T X\]

for a given vector of systematic components $X$ and predictor variables $\theta$. Write the mathematical expression for the hyperplane that describes the decision boundary

Answer

\[\theta_0 + \theta^T X = 0\]

The Sigmoid

Question

True or False: The logit function and the natural logistic (sigmoid) function are inverses of each other.

Answer

True

\[z(p) = logit(p) = log(\frac{p}{1 - p})\] \[p(z) = \frac{exp z}{1 + exp z}\]

Question

Compute the derivative of the natural sigmoid function:

\[\sigma (x) = \frac{1}{1 + e^{-x}} \in (0, 1)\]

Answer

\[\frac{d}{dx} \sigma(x) = \frac{d}{dx}((1 + e^{-x})^{-1}) = -((1 + e^{-x})^{(-2)})\frac{d}{dx}(1 + e^{-x}) = \frac{e^{-x}}{(1 + e^{-x})^2}\] \[{f}'(\theta_i) = f(\theta_i)(1 - f(\theta_i))\]

Question

Remember that in logistic regression, the hypothesis function for some parameter vector $\beta$ and measurement vector $x$ is defined as:

\[h_\beta (x) = g(\beta^T x) = \frac{1}{1 + e^{-\beta^T x}}\] \[= P(y = 1 | x; \beta)\]

Suppose the coefficients of a logistic regression model with independent variables are as follows: $\beta_0 = −1.5, \beta_1 = 3, \beta_2 = −0.5$. Assume additionally, that we have an observation with the following values for the dependent variables: $x_1 = 1, x_2 = 5$. As a result, the logit equation becomes:

\[logit = \beta_0 + \beta_1 x_1 + \beta_2 x_2\]

What is the value of the logit for this observation?
What is the value of the odds for this observation?
What is the value of $P(y = 1)$ for this observation?

Answer

\[logit = \beta_0 + \beta_1 x_1 + \beta_2 x_2 = -1.4 + 3 \cdot 1 + -0.5 \cdot 5 = -1\]
\[odds = e^{logit} = e^{-1} = 0.3678794\]
\[P(y = 1) = \frac{1}{1 + e^{-logit}} = \frac{1}{1 + e^{1}} = 0.2689414\]

\[odds = \frac{P(y = 1)}{P(y = 0)}\]

Truly Understanding Logistic Regression

Question

암의 종류에 따른 암 치료 성공률에 대한 통계를 해석하는 문제(RR과 OR, CI를 사용하여 해석)

Proton therapy (PT) is a widely adopted form of treatment for many types of cancer including breast and lung cancer.

A PT device that was not properly calibrated is used to simulate the treatment of cancer. As a result, the PT beam does not behave normally. A data scientist collects information relating to this simulation. The covariates presented in Table are collected during the experiment. The columns Yes and No indicate if the tumour was eradicated or not, respectively.

               Tumour eradication
Cancer Type    Yes      No
Breast         560      260
Lung           69       36

What is the explanatory variable and what is the response variable?
Explain the use of relative risk and odds ratio for measuring association.
Are the two variables positively or negatively associated? Find the direction and strength of the association using both relative risk and odds ratio.
Compute a 95% confidence interval (CI) for the measure of association.
Interpret the results and explain their significance.

Answer

Tumour eradication is the response variable and cancer type is the explanatory variable.
Relative risk (RR) is the ratio of risk of an event in one group (e.g., exposed group) versus the risk of the event in the other group (e.g., non-exposed group). The odds ratio (OR) is the ratio of odds of an event in one group versus the odds of the event in the other group.
If we calculate odds ratio as a measure of association:

\[OR = \hat{\theta} = \frac{Lung 암이 근절될 odds}{Breast 암이 근절될 odds} = \frac{560 \times 36}{69 \times 260} = 1.23745\]

And the log-odds ratio is $(log(1.23745)) = 0.213052$: The odds ratio is larger than one, indicating that the odds for a breast cancer is more than the odds for a lung cancer to be eradicated. Notice however, that this result is too close to one, which prevents conclusive decision regarding the odds relation. Additionally, if we calculate relative risk as a measure of association:

\[RR = \frac{560 / (560 + 260)}{69 / (69 + 36)} = 1.0392\]

The 95% confidence interval for the odds-ratio, $\theta$ is computed from the sample confidence interval for log odds ratio:

\[\hat{\sigma} (log(\hat{\theta})) = \sqrt{\frac{1}{560} + \frac{1}{260} + \frac{1}{69} + \frac{1}{36}} = 0.21886\]

Therefore, the 95% CI for $log(\theta)$ is:

\[0.213052 ± 1.95 × 0.21886 = (0.6398298, −0.2137241)\]

Therefore, the 95% CI for $\theta$ is:

\[(e^{-0.210}, e^{0.647}) = (0.810, 1.909)\]

The CI (0.810, 1.909) contains 1, which indicates that the true odds ratio is not significantly different from 1 and there is not enough evidence that tumour eradication is dependent on cancer type.

Question

Consider a system for radiation therapy planning. Given a patient with a malignant tumour, the problem is to select the optimal radiation exposure time for that patient. A key element in this problem is estimating the probability that a given tumour will be eradicated given certain covariates. A data scientist collects information relating to this radiation therapy system.

The following covariates are collected; $X_1$ denotes time in milliseconds that a patient is irradiated with, $X_2$ = holds the size of the tumour in centimeters, and $Y$ notates a binary response variable indicating if the tumour was eradicated. Assume that each response’ variable $Y_i$ is a Bernoulli random variable with success parameter $p_i$ , which holds:

\[p_i = \frac{e^{\beta_0 + \beta_1 x_1 + \beta_2 x_2}}{1 + e^{\beta_0 + beta_1 x_1 + \beta_2 + x_2}}\]

The data scientist fits a logistic regression model to the dependent measurements and produces these estimated coefficients:

\[\hat{\beta_0} = -6\] \[\hat{\beta_1} = 0.05\] \[\hat{\beta_2} = 1\]

Estimate the probability that, given a patient who undergoes the treatment for 40 milliseconds and who is presented with a tumour sized 3.5 centimetres, the system eradicates the tumour.
How many milliseconds the patient in part (a) would need to be radiated with to have exactly a 50% chance of eradicating the tumour?

Answer

\[\hat{p}(X) = \frac{e^{-6 + 0.05 X_1 + X_2}}{1 + e^{-6 + -0.05 X_1 + X_2}} = 0.3775\]

\[\frac{e^{-6 + 0.05 X_1 + 3.5}}{1 + e^{-6 + 0.05 X_1 + 3.5}} = 0.5\] \[e^{-6 + 0.05 X_1 + 3.5} = 1\] \[X_1 = \frac{2.5}{0.05} = 50\]

Question

치과용 아말감에 뜨거운 커피가 닿으면 수은 증기의 방출을 자극한다.

편두통이 수은 증기의 방출과 관련이 있는지를 확인

Recent research suggests that heating mercury containing dental amalgams may cause the release of toxic mercury fumes into the human airways. It is also presumed that drinking hot coffee, stimulates the release of mercury vapour from amalgam fillings.

To study factors that affect migraines, and in particular, patients who have at least four dental amalgams in their mouth, a data scientist collects data from 200K users with and without dental amalgams. The data scientist then fits a logistic regression model with an indicator of a second migraine within a time frame of one hour after the onset of the first migraine, as the binary response variable (e.g., migraine=1, no migraine=0). The data scientist believes that the frequency of migraines may be related to the release of toxic mercury fumes. There are two independent variables:

X1 = 1 if the patient has at least four amalgams; 0 otherwise.
X2 = coffee consumption (0 to 100 hot cups per month). The output from training a logistic regression classifier is as follows:

Analysis of LR Parameter Estimates
Parameter    Estimate    Std.Err    Z-val     Pr>|Z|
Intercept    -6.36347    3.21362    -1.980    0.0477
$X_1$        -1.02411    1.17101    -0.875    0.3818
$X_2$        0.11904     0.05497    2.165     0.0304

Using $X_1$ and $X_2$, express the odds of a patient having a migraine for a second time.
Calculate the probability of a second migraine for a patient that has at least four amalgams and drank 100 cups per month?
For users that have at least four amalgams, is high coffee intake associated with an increased probability of a second migraine?
Is there statistical evidence that having more than four amalgams is directly associated with a reduction in the probability of a second migraine?

Answer

\[z(X_1, X_2) = -6.36 - 1.02 \times X_1 + 0.12 \times X_2\]

\[odds = exp(z(X_1, X_2))\]
\[p = exp(z(1, 100)) / (1 + exp(z(1, 100))) = 0.99\]
Yes. The coefficient for coffee consumption is positive (0.119) and the p-value is less than 0.05 (0.0304).
No. The p-value for this predictor is 0.3818 > 0.05

Question

알츠하이머와 잇몸질환의 연관성

To study factors that affect Alzheimer’s disease using logistic regression, a researcher considers the link between gum (periodontal) disease and Alzheimer as a plausible risk factor. The predictor variable is a count of gum bacteria in the mouth.

The response variable, $Y$ , measures whether the patient shows any remission (e.g. yes=1). The output from training a logistic regression classifier is as follows:

Parameter       DF     Estimate     Std
Intercept        1    -4.8792       1.2197
gum bacteria     1     0.0258       0.0194

Estimate the probability of improvement when the count of gum bacteria of a patient is 33.
Find out the gum bacteria count at which the estimated probability of improvement is 0.5.
Find out the estimated odds ratio of improvement for an increase of 1 in the total gum bacteria count.

Answer

\[\hat{\pi}(gum bacteria) = \frac{exp(-4.8792 + 0.0258 \times gum bacteria)}{1 + exp(-4.8792 + 0.0258 \times gum bacteria)}\] \[\hat{\pi}(33) = 0.01748\]

\[\hat{\pi}(gum bacteria) = 0.5\] \[\hat{\pi}(gum bacteria) = \frac{exp(\hat{\alpha} + \hat{\beta} x)}{1 + exp(\hat{\alpha} + \hat{\beta} x)} = 0.5\] \[gum bacteria = x = -\hat{\alpha} / \hat{\beta} = 4.8792 / 0.0258 = 189.116\]

\[exp(\hat{\beta}) = exp(0.0258) = 1.0504\]

The Logit Function and Entropy

Question

The entropy of a single binary outcome with probability p to receive 1 is defined as:

\[H(p) ≡ −p log p − (1 − p) log(1 − p)\]

At what $p$ does $H(p)$ attain its maximum value?
What is the relationship between the entropy $H(p)$ and the logit function, given $p$?

Answer

The entropy has a maximum value of $log_{2}(2)$ for probability $p = 1/2$, which is the most chaotic distribution. A lower entropy is a more predictable outcome, with zero providing full certainty
The derivative of the entropy with respect to $p$ yields the negative of the logit function:

\[\frac{dH(p)}{dp} = -logit(p)\]

Python/PyTorch/CPP

Question

  
#include ...
std::vector<double> theta {-6,0.05,1.0};           # 2

double sigmoid(double x) {
  double tmp =1.0 / (1.0 + exp(-x));
  std::cout << "prob=" << tmp<<std::endl;
  return tmp;
}

double hypothesis(std::vector<double> x){
  double z;
  z=std::inner_product(std::begin(x), std::end(x), # 10
    → std::begin(theta), 0.0);
  std::cout << "inner_product=" << z<<std::endl;
  return sigmoid(z);
}

int classify(std::vector<double> x){
  int hypo=hypothesis(x) > 0.5f;                   # 15
  std::cout << "hypo=" << hypo<<std::endl;
  return hypo;
}

int main() {
  std::vector<double> x1 {1,40,3.5};
  classify(x1);
}

Explain the purpose of line 10, i.e., $inner_product$.
Explain the purpose of line 15, i.e., $hypo(x) > 0.5f$.
What does $\theta$ (theta) stand for in line 2?
Compile and run the code, you can use: https://repl.it/languages/cpp11 to evaluate the code. What is the output?

Answer

During inference, the purpose of inner_product is to multiply the vector of logistic regression coefficients with the vector of the input which we like to evaluate, e.g., calculate the probability and binary class.
The line hypo(x) > 0.5f is commonly used for the evaluation of binary classification wherein probability values above 0.5 (i.e., a threshold) are regarded as TRUE whereas values below 0.5 are regarded as FALSE.
The term $\theta$ (theta) stands for the logistic regression coefficients which were evaluated during training.

The output is as follows:

> inner_product=-0.5
> prob=0.377541
> hypo=0

Question

  
import torch
import torch.nn as nn

lin = nn.Linear(5, 7)
data = (torch.randn(3, 5))

print(lin(data).shape)

Answer

  
> torch.Size([3, 7])

Question

  
from scipy.special import expit
import numpy as np
import math

def Func001(x):
  e_x = np.exp(x - np.max(x))
  return e_x / e_x.sum()

def Func002(x):
  return 1 / (1 + math.exp(-x))

def Func003(x):
  return x * (1-x)

Analyse the methods Func001, Func002 and Func003 presented in script, find their purposes and name them.

Answer

A softmax function
A sigmoid function
A derivative of a sigmoid function

Question

  
from scipy.special import expit
import numpy as np
import math

def Func006(y_hat, y):
  if y == 1:
    return -np.log(y_hat)
  else:
    return -np.log(1 - y_hat)

Analyse the method Func006 presented in script. What important concept in machine-learning does it implement?

Answer

binary cross-entropy function.

Question

  
from scipy.special import expit
import numpy as np
import math

def Ver001(x):
  return 1 / (1 + math.exp(-x))

def Ver002(x):
  return 1 / (1 + (np.exp(-x)))

WHO_AM_I = 709

def Ver003(x):
  return 1 / (1 + np.exp(-(np.clip(x, -WHO_AM_I, None))))

Which mathematical function do these methods implement?
What is significant about the number 709 in line 11?
Given a choice, which method would you use?

Answer

All the methods are variations of the sigmoid function.
In Python, approximately 1.797e + 308 holds the largest possible valve for a floating point variable. The logarithm of which is evaluated at 709.78. If you try to execute the following expression in Python, it will result in inf : np.log(1.8e + 308).
I would use Ver003 because of its stability.

정리

odds = 실패 대비 성공 확인

logit = log + odds

odds는 그 값이 1보다 큰지가 결정의 기준이고, logit은 0보다 큰지가 결정의 기준.

\[p = [0, 1]\] \[odds(p) = [0, \infty]\] \[logit(p) = [-\infty, \infty]\]

logit의 역함수는 sigmoid입니다.

sigmoid를 K개의 클래스로 일반화 하면 softmax

softmax를 2개의 클래스로 일반화 하면 sigmoid

RR = 상대 위험도 OR = 승산비(odds의 비율)

\[RR = \frac{a / (a + b)}{c / (c + d)}\]

위험인자 노출된 사람은 암에 걸릴 확률이 RR배 더 높음

\[OR = \frac{a / b}{c / d}\]

위험인자에 노출된 사람은 노출되지 않은 사람에 비해 OR배 정도 더 암에 걸리는 경향을 보임

1) OR=1 인 경우:

위험요인에 노출되는 것이 질병 발생에 유의미한 영향을 준다고 볼 수 없습니다.

2) OR>1 인 경우:

위험요인에 노출되었을 때 질병이 발생할 오즈가 노출되지 않은 경우보다 몇 배 더 높다고 말합니다.

예를 들어 담배를 피웠을 때 폐암에 걸릴 OR=2라고 한다면,

담배를 피지 않은 경우보다 담배를 핀 경우에 폐암에 걸릴 오즈가 2배라고 해석하게 됩니다.

3) OR<1 인 경우:

위의 2번과 반대로 해석하면 됩니다.

귀무가설 : 연구자가 부정하는 가설

대립가설 : 연구자가 주장하는 가설

confidence interval = 신뢰 구간(나 작업하는데 5 ~ 10분 정도 걸려 ㅜ)

p value = p-value란 뽑은 데이터가 얼마나 실제로 그럴듯한 데이터인지(귀무가설을 따르는지)를 나타내는 확률

p < 0.05 : 100번의 실험을 했을 때 93번의 실험이 연구자의 가설대로 재현이 되었고 5번의 예외적 경우가 있었음. 해당 데이터는 신뢰도가 높고 유의미한 데이터이다.

사용할 수 있는 가장 큰 숫자는 1.7976931348623157E + 308, 로그는 약 709.782

2.2250738585072014e-308에서 1.7976931348623157e+308까지 표현

PROBABILISTIC PROGRAMMING & BAYESIAN DL

Expectation and Variance

Question

Define what is meant by a Bernoulli trial.

Answer

Bernoulli : 이진 분류

The notion of a Bernoulli trial refers to an experiment with two dichotomous binary outcomes; success (x = 1), and failure (x = 0)

Question

The binomial distribution is often used to model the probability that k out of a group of $n$ objects bare a specific characteristic. Define what is meant by a binomial random variable $X$.

Answer

A binomial random variable $X = k$ represents $k$ successes in n mutually independent Bernoulli trials.

Question

What does the following shorthand stand for?

\[X \sim Binomial(n, p)\]

Answer

The shorthand $X ∼ Binomial(n, p)$ indicates that the random variable X has the binomial distribution. The positive integer parameter n indicates the number of Bernoulli trials and the real parameter $p$, $0 < p < 1$ holds the probability of success in each of these trials.

Question

Find the probability mass function (PMF) of the following random variable:

\[X \sim Binomial(n, p)\]

Answer

The random variable $X \sim Binomial(n, p)$ has the following PMF:

\[P(X = k) = \binom{n}{k} p^k (1 - p)^{n - k}; k = 0, 1, 2, \dots, n.\]

Question Answer the following questions:

Define what is meant by (mathematical) expectation.
Define what is meant by variance.
Derive the expectation and variance of a the binomial random variable $X \sim Binomial(n, p)$ in terms of $p$ and $n$.

Answer

For a random variable $X$ with probability mass function $P(X = k)$ and a set of outcomes $K$, the expected value of $X$ is defined as:

\[E[X] := \sum_{k \in K} k P(X = k)\]

Note. The expectation of $X$ may also be denoted by $\mu_X$

The vaiance of $X$ is defined as:

\[Var[x] := E[(X - E[X])^2]\]

Note. The variance of $X$ may also be denoted by $\sigma^2_X$, while $\sigma_X$ itself denotes the standard deviation of $X$.

The population mean and variance of a binomial random variable with parameters $n$ and $p$ are:

\[E[X] = np\] \[V[X] = np(1 - p)\]

Question

Proton therapy (PT) is a widely adopted form of treatment for many types of cancer. A PT device which was not properly calibrated is used to treat a patient with pancreatic cancer. As a result, a PT beam randomly shoots 200 particles independently and correctly hits cancerous cells with a probability of 0.1.

Find the statistical distribution of the number of correct hits on cancerous cells in the described experiment. What are the expectation and variance of the corresponding random variable?
A radiologist using the device claims he was able to hit exactly 60 cancerous cells. How likely is it that he is wrong?

Answer

\[X \sim Binomial(200, 0.1)\]

Expectation : $x = E(x) = 200 \times 0.1 = 20$

Variance : $Var = 200 \times 0.10(1 - 0.10) = 18.0$

Here we propose two distinguished methods to answer the question. Primarily, the straightforward solution is to employ the definition of the binomial distribution and substitute the value of $X$ in it. Namely:

\[P(X = 60; n = 200, p = 0.1)\] \[= \binom{200}{60} 0.1^{60} (1 - 0.1)^{200 - 60}\] \[= \approx 2.7 \times e^{-15}\]

This leads to an extremely high probability that the radiologist is mistaken.

The following approach is longer and more advanced, but grants the reader with insights and intuition regarding the results. To derive how wrong the radiologist is, we can employ an approximation by considering the standard normal distribution. In statistics, the Z-score allows us to understand how far from the mean is a data point in units of standard deviation, thus revealing how likely it is to occur.

Therefore, the probability of correctly hitting 60 cells is:

\[z = \frac{x - \mu}{\sigma}\] \[P(X \geq 60) = P(Z \geq \frac{60 - 20}{\sqrt{18.0}}) = P(Z \geq 9.428) \approx 0\]

Again, the outcome shows the likelihood that the radiologist was wrong approaches 1.

Conditional Probability

Question

사건 B가 일어나는 경우에 사건 A가 일어날 확률

Given two events $A$ and $B$ in probability space $H$, which occur with probabilities $P(A)$ and $P(B)$, respectively:

Define the conditional probability of $A$ given $B$. Mind singular cases.
Annotate each part of the conditional probability formulae.

Answer

For two event $A$ and $B$ with $P(B) > 0$, the conditional probability of $A$ given that $B$ has ocurred is defined as:

\[P(A | B) = \frac{P(A \cap B)}{P(B)}\]

It is easy to note that if $P(B) = 0$, this relation is not defined mathematically. In this case, $$P(A

B) = P(A \cap B) = P(A)$$

\[P(A | B) = \frac{P(A \cap B)}{P(B)}\]

\[P(A | B) = A given B\]
\[P(A \cap B) = A and B\]
\[P(B) = B only\]

Question

Bayesian inference amalgamates data information in the likelihood function with known prior information. This is done by conditioning the prior on the likelihood using the Bayes formulae. Assume two events $A$ and $B$ in probability space $H$, which occur with probabilities $P(A)$ and $P(B)$, respectively. Given that $A \cup B = H$, state the Bayes formulae for this case, interpret its components and annotate them.

Answer

Question

Define the terms likelihood and log-likelihood of a discrete random variable $X$ given a fixed parameter of interest $\gamma$. Give a practical example of such scenario and derive its likelihood and log-likelihood.

Answer

Question

Define the term prior distribution of a likelihood parameter $\gamma$ in the continuous case.

Answer

Question

Show the relationship between the prior, posterior and likelihood probabilities

Answer

Question

In a Bayesian context, if a first experiment is conducted, and then another experiment is followed, what does the posterior become for the next experiment?

Answer

Question

What is the condition under which two events $A$ and $B$ are said to be statistically independent?

Answer

Rayes Rule

Question

In an experiment conducted in the field of particle physics (Fig. 3.2), a certain particle may be in two distinct equally probable quantum states: integer spin or half-integer spin. It is well-known that particles with integer spin are bosons, while particles with half-integer spin are fermions.

A physicist is observing two such particles, while at least one of which is in a half-integer state. What is the probability that both particles are fermions?

Answer

Question

During pregnancy, the Placenta Chorion Test is commonly used for the diagnosis of hereditary diseases. The test has a probability of 0.95 of being correct whether or not a hereditary disease is present.

It is known that 1% of pregnancies result in hereditary diseases. Calculate the probability of a test indicating that a hereditary disease is present.

Answer

Question

The Dercum disease is an extremely rare disorder of multiple painful tissue growths. In a population in which the ratio of females to males is equal, 5% of females and 0.25% of males have the Dercum disease.

A person is chosen at random and that person has the Dercum disease. Calculate the probability that the person is female.

Answer

Question

Answer

Question

Answer

Question

Answer

정리

참조

사건을 $n$회 시행하고, 성공 확률이 $p$라면 평균적으로 $np$번 성공하는 것이 맞을 것 같다.

가령, 100회 동전을 던졌을 때 50번은 앞면이 나올 것이라고 보는 것이 상식적이다.

HIGH SCHOOL

Logarithms in Information Theory

Question

First law

\[log A + log B = log AB\] \[log_10 3 + log_10 4\]

Second law

\[log A^n = n log A\] \[log_2 4^6\]

Third law

\[log A - log B = log \frac{A}{B}\] \[log_e 15 - log_e 3\]

Answer

\[log_10 12\]
\[6 log_2 4\]
\[log_e 5\]

Shannon’s Entropy

Question

Write Shannon’s famous general formulae for uncertainty.

Answer

\[H = \sum_{a=1}^N P_a log_2 P_a\]

Question

For an event which is certain to happen, what is the entropy?
For $N$ equiprobable events, what is the entropy?

Answer

0
\[log_2(N)\]

Question

Shannon found that entropy was the only function satisfying three natural properties. Enumerate these properties.

Answer

$H(X)$ is always non-negative, since information cannot be lost.
The uniform distribution maximizes $H(X)$, since it also maximizes uncertainty.
The additivity property which relates the sum of entropies of two independent events. For instance, in thermodynamics, the total entropy of two isolated systems which coexist in equilibrium is the sum of the entropies of each system in isolation.

엔트로피는 손실이 없기 때문에 음수가 될 수 없다.

uniform distribution은 불확실성이 최대화되기 때문에 엔트로피를 최대화한다.

독립된 사건일 때 총 엔트로피는 각 독립된 사건의 엔트로피 합으로 정의한다.

Question

In information theory, minus the logarithm of the probability of a symbol (essentially the number of bits required to represent it efficiently in a binary code) is defined to be the information conveyed by transmitting that symbol. In this context, the entropy can be interpreted as the expected information conveyed by transmitting a single symbol from an alphabet in which the symbols occur with the probabilities $\pi_k$.

Mark the correct answer: Information is a/an [decrease/increase] in uncertainty.

Answer

increase

Question

Claud Shannon’s paper “A mathematical theory of communication”, marked the birth of information theory. Published in 1948, it has become since the Magna Carta of the information age. Describe in your own words what is meant by the term Shannon bit.

Answer

The Shannon bit has two distinctive states; it is either 0 or 1, but never both at the same time. Shannon devised an experiment in which there is a question whose only two possible answers were equally likely to happen.

He then defined one bit as the amount of information gained (or alternatively, the amount of entropy removed) once an answer to the question has been learned. He then continued to state that when the a-priori probability of any one possible answer is higher than the other, the answer would have conveyed less than one bit of information.

Question

With respect to the notion of surprise in the context of information theory:

Define what it actually meant by being surprised.
Describe how it is relted to the likelihood of an event happening.
True or False: The less likely the occurrence of an event, the smaller information it conveys.

Answer

The notion of surprise is directly related to the likelihood of an event happening. Mathematically is it inversely proportional to the probability of that event. Accordingly, learning that a high-probability event has taken place, for instance the sun rising, is much less of a surprise and gives less information than learning that a low-probability event, for instance, rain in a hot summer day, has taken place. Therefore, the less likely the occurrence of an event, the greater information it conveys. In the case where an event is a-priori known to occur for certain ($P_a = 1$), then no information is conveyed by it. On the other hand, an extremely intermittent event conveys a lot of information as it surprises us and informs us that a very improbable state exists. Therefore, the statement in part 3 is false.

Question

Assume a source of signals that transmits a given message $a$ with probability $P_a$. Assume further that the message is encoded into an ordered series of ones and zeros (a bit string) and that a receiver has a decoder that converts the bit string back into its respective message. Shannon devised a formulae that describes the size that the mean length of the bit string can be compressed to. Write the formulae.

Answer

This quantity $I_{Sh}$, represented in the formulae is called the Shannon information of the source:

\[I_{Sh} = - \sum_a p_a log_2 p_a\]

It refers to the mean length in bits, per message, into which the messages can be compressed to. It is then possible for a communications channel to transmit $I_{Sh}$ bits per message with a capacity of $I_{Sh}$.

Question

Answer the follwing questions:

Assume a source that provides a constant stream of $N$ equally likely symbols ${ x_1, x_2, \dots, x_N}$. What does Shannon’s formulae reduce to in this particular case?
Assume that each equiprobable pixel in a monochrome image that is fed to a DL classification pipeline, can have values ranging from 0 to 255. Find the entropy in bits.

Answer

Question

Given Shannon’s famous general formulae for uncertainty.

\[H = - \sum_{a = 1}^{N} P_a log_2 P_a\]

Plot a graph of the curve of probability vs. uncertainty.
Complete the sentence: The curve is [symmetrical/asymmetrical]
Complete the sentence: The curve rises to a [minimum/maximum] when the two symbols are equally likely ($P_a = 0.5$).

Answer

Question

Assume we are provided with biased coin for which the event ‘heads’ is assigned probability $p$, and ‘tails’ - a probability of $1 − p$. Using $H = - \sum_{a = 1}^{N} P_a log_2 P_a$, the respective entropy is:

\[H = - p log p - (1 - p) log (1 - p)\]

Therefore, $H \geq 0$ and the maximum possible uncertainty is attained when $p = 1/2$, is $H_{max} = log_2 2$.

Given the above formulation, describe a helpful property of the entropy that follows from the concavity of the logarithmic function.

Answer

Question

True or False: Given random variables $X$, $Y$ and $Z$ where $Y = X + Z$ then:

\[H(X, Y) = H(X, Z)\]

Answer

Question

What is the entropy of a biased coin? Suppose a coin is biased such that the probability of ‘heads’ is $p(x_h) = 0.98$.

Complete the sentence: We can predict ‘heads’ for each flip with an accuracy of [__]%.
Complete the sentence: If the result of the coin toss is ‘heads’, the amount of Shannon information gained is [__] bits.
Complete the sentence: If the result of the coin toss is ‘tails’, the amount of Shannon information gained is [__] bits.
Complete the sentence: It is always true that the more information is associated with an outcome, the [more/less] surprising it is.
Provided that the ratio of tosses resulting in ‘heads’ is $p(x_h)$, and the ratio of tosses resulting in ‘tails’ is $p(xt)$, and also provided that $p(x_h)+p(x_t) = 1$, what is formulae for the average surprise?
What is the value of the average surprise in bits?

Answer

concept

This post is licensed under CC BY 4.0 by the author.