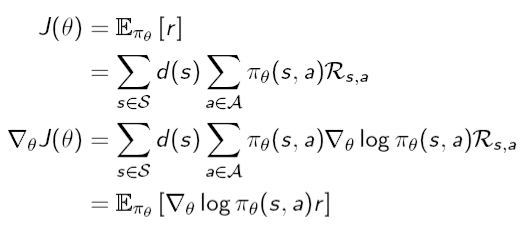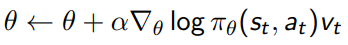Post

강화학습 끄적이기 2

Posted
By Jaemin Jeong
16 min read

Reinforcement

강화학습의 개념을 순차적으로 정리

  • Q-learning
  • Q-Network
  • DQN
  • Policy Gradient

강화학습의 개념

머신러닝의 한 영역으로 미래의 보상을 위해서 스스로 의사결정 할 수 있게 하는 학습방법이다.

1
2
3
4
5
6
7
8

환경
-------------------------------
   S1    S2    S3    S4
-------------------------------
|  0  |  0  |  0  |  0  |  R  |
-------------------------------

환경(E)이 존재하고 그 환경에는 어떠한 보상(R)이 존재한다. 그 보상을 얻기 위해서는 어떠한 행동(A)를 취해야 한다. 위와 같은 환경에서는 오른쪽으로 갔을때 보상을 얻을 수 있다. 하지만 이것은 우리가 눈으로 볼때는 알 수 있지만 컴퓨터 자체는 안에 있는 값만을 이용해서 알아야 한다.그 때문에 컴퓨터가 스스로 어떠한 정책(P)을 학습하게 하는 것이 강화학습이다.

Q-learning

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

환경
-------------------------------
   S1    S2    S3    S4
-------------------------------
|  0  |  0  |  0  |  0  |  R  |
-------------------------------

Q-table : 안쪽에 action에 대한 Q-value 값이 채워진다.
          ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
           |  S1  |  S2  |  S3  |  S4  |  S5  |
          ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
왼쪽     |   0   |   0   |   0   |   0   |   0   |
           ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
오른쪽  |  0.1  |  0.3  |  0.5  |  0.7  |  0  |
           ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ

Q의 value를 이용한 첫번째 강화학습은 Q-table을 이용한 Q-learning이다. 처음에는 왼쪽으로 갈지 오른쪽으로 갈지 모르기 때문에 랜덤으로 행동을 해가면서 보상을 얻기위해 이곳 저곳 움직인다. 그리고 최종적으로 보상에 도달하면 Q-table에 있는 Q-value를 업데이트 하면서 다음에 보상을 찾아가는데 도움을 준다.

이것을 간략한 공식 형태로 표현을 하면

1

state, action => Q => reward

이러한 형태가 된다. Q는 어떠한 상태에서 특정한 행동을 취할 때 보상을 얼마나 받을 수 있는지에 대한 지표가 된다. 그러면 이 Q가 어떠한 행동을 했을때 다음상태에서 보상이 최대가 되는 값을 알고있기 때문에 Q를 따라서 이동한다.

1

max Q

Q의 다음상태의 최대값도 Q-table을 이용해서 알 수 있기 때문에 다음상태에 대해서 다음 행동을 취한 값중 최대값을 보상과 합해서 Q가 어디로 행동해야 할지를 예측한다.

1
2
3
4

내가 있는 상태 : s
나의 행동 : a
다음 상태 : s`
내가 있는 상태에서 행동 하였을 때 보상 : r

Q-learning의 공식

1

Q(s,a) = r + maxQ(s`,a`)

위 공식에 의해서 최대값을 전부다 보상으로 하면 특정 루트에만 최적화가 되기 때문에 GAMMA를 추가시켜서 아래 공식을 만든다.

1

Q(s,a) = r + (GAMMA)*maxQ(s`,a`)

그리고 위의 모든 경우는 항상 정해져 있는 환경인 경우에서 특화되어서 설명하였다. 하지만 환경은 항상 고정적이지 않고 유동적인 변화가 많다.

예를들어서 얼음에서 미끄러지는 즉, Q가 알수없는 행동이 이와 같다. 얼음에서 미끄러지는 경우 내가 오른쪽으로 갔을때 성공했는데 얼음에서 미끄러져서 2칸을 가버려 실패할 경우 Q는 그 환경에 대한 유동적인 변화에 대해서 까지 학습하지 않는다.

그렇기 때문에 Q-table의 값을 다 받아들여서 Q-value를 만들지 말고 내가 가고싶은 방향에 어느정도에 영향을 줄지에 대한 learning rate를 설정시켜 공식을 최종으로 만든다.

\[Q(s,a) = (1-\alpha)Q(s,a) + \alpha[r + \gamma maxQ(s^{\prime},a^{\prime})]\]

Q-Network

Q-table은 너무 많은 행동이 있고 환경이 하나의 이미지로 있는 경우에 Q-tabel이 기하급수적으로 커지는 현상이 발생해 아예 접근조차 못하는 경우가 있다.(예를 들어 Atari game) 그래서 이러한 모든 경우의 수를 전부 고려하기 어려운 문제를 Neural Network를 이용해서 표현한다.

1

state -> model -> Q value

위와 같이 어떠한 상태가 모델에 들어가면 모든 행동에 대한 값을 예측하고 그 중 최대값을 선택하면 어떤 행동을 취했을 때 보상을 최대로 하는지에 대해 알 수 있다. 그래서 이에 대한 학습의 loss는 아래와 같이 표현된다.

1
2
3
4

loss = (pred - target)^2

target = r + (GAMMA)*maxQ(s`,a` | theta)
pred = Q(s,a | theta)
\[min \sum_{t=0}^{T}[\hat{Q}(s,a | \theta) - \gamma max \hat{Q}(s^{\prime},a^{\prime} | \theta)]^2\]

위에서 말한 것들을 알고리즘으로 정리하면

  1. state를 Network에 넣고 value를 출력으로 받는다.
  2. value를 최대로 하는 action을 선택한다.
  3. action을 통해서 다음 state와 reward를 받는다.
  4. 위에 정의한 공식을 통해 보상을 최대로하는 \(\theta\)를 업데이트 한다.

DQN

위에서 설명한 Q-Network에는 두가지 문제점이 있다.

  1. 현재 행동과 다음 행동이 유사한 경우에 학습이 잘되지않는다.

  2. target과 pred가 가중치를 공유하기 때문에 학습이 불안정하다.

이를 해결하기 위해서 DQN은 두가지 방법을 제안한다.

  1. memory의 개념으로 보상,현재상태,다음상태,행동을 memory에 쌓고 그것을 랜덤하게 샘플링해서 학습시킨다. 랜덤하게 샘플링해도 분포가 비슷하기 때문에 결국 수렴하게 되어있다.

  2. 네트워크를 target과 pred를 분리시키고 pred 부분의 가중치만 업데이트 하면서 어느정도 학습을 진행할때 그 가중치를 target 네트워크에 복사한다.

위와 같은 방법으로 Q-Network를 해결하며 Nature 논문에도 실릴 정도로 실용적이지만 간단한 방법이다.

\[min \sum_{t=0}^{T}[\hat{Q}(s,a | \theta) - \gamma max \hat{Q}(s^{\prime},a^{\prime} | \bar\theta)]^2\]

공식은 위와같이 간단하고 알고리즘으로 정리하면

  1. D크기를 가지는 memory와 \(\theta\) \(\bar\theta\)를 정의한다.(둘은 처음에는 같다.)

  2. action을 선택하고 \(s,s^{\prime},a,r\)을 memory에 업데이트 한다.

  3. memory를 random sampling으로 추출해서 학습한다.

  4. 위에 정의한 공식으로 보상을 최대로하는 \(\theta\)를 업데이트 한다.

  5. C스탭후에 \(\bar\theta\)에 \(\theta\)를 복사한다.

Policy Gradient

여태까지는 네트워크에서 state를 입력으로 받고 Q의 value값이 출력이었다. 그리고 그 Q-value값으로 보상을 최대로 하는 action을 선택했다. 이러한 방식을 value-based reinforcement라고 한다. value-based reinforcement에서는 2가지 단점이있다.

  1. value function이 약간만 달라져도 policy 자체는 왼쪽으로 가다가 오른쪽으로 간다던지 크게 변화한다. 그래서 최적값에 수렴하는데 불안정하다.

  2. 때로는 가위바위보와 같은 게임이 있을 수 있다. 가위바위보는 확률적인 문제로 1/3씩 동등한 확률로 가위바위보를 하는게 최적의 policy이다. 하지만 value-based는 Q-value값을 통해 하나의 action만 선택하는 방법이기 때문에 이러한 문제에 취약하다.

그래서 지금부터 설명할 policy-based reinforcement는 출력이 policy인 방법이다. policy는 A라는 상황이 있을때 B라고 행동하라는 정책이고 이러한 정책을 학습하기 위해서는 object function이라는 것을 정의해야한다. 이 object function을 정의하는 3가지 방법이있다.

  • start value 사용
\[J_1(\theta) = V^{\pi_\theta}(s_1) = \mathbb{E}_{\pi_\theta}[v_1]\]
  • 지속적인 환경에서 값의 평균을 사용
\[J_{avV}(\theta) = \sum_s d^{\pi_\theta}(s) V^{\pi_\theta}(s)\]
  • 매 step마다 보상의 평균값을 사용
\[J_{avR}(\theta) = \sum_s d^{\pi_\theta}(s) \sum_a \pi_\theta(s,a)R^a_s\]

\(d^{\pi_{\theta}}(s)\)는 \(\pi_\theta\)를 위한 Markov chain의 stationary distribution

Markov chain은 상태값의 시퀀스에서 현재 상태는 전 상태에만 영향을 받는다는 가정이다. 예를들어서 우리의 날씨 Markov chain에는 총 4가지의 상태 전이확률(Transition Probabilities)이 있다.

1
2
3
4
5

P(맑음 | 맑음), P(비 | 맑음), P(맑음 | 비), P(비 | 비)
P(맑음 | 맑음) = 0.3
P(비 | 맑음) = 0.7
P(맑음 | 비) = 0.1
P(비 | 비) = 0.9

날씨로 생각하면 오늘 상태로 내일 상태의 날씨확률을 계산하고 그 확률로 내일 모레의 날씨의 확률분포를 계산할 수 있다. 예를 들어 오늘 날씨가 맑을 때 내일이 비가오고 모레가 맑을 확률은

1
2
3
4

P(비,맑음 | 맑음)
= P(맑음 | 비, 맑음)*P(비 | 맑음) = P(맑음 | 비)*P(비 | 맑음) <- markov chain
= 0.1*0.7
= 0.07

이러한 과정을 반복하면 어느 순간부터 그날의 날씨 확률분포가 그 전날과 같아지는 때가 온다. 이러한 상태에 도달한 날씨의 확률분포를 stationary distribution 이라고 한다.

결론은, policy gradient의 목표는 이러한 object function을 최대화시키는 \(\theta\)값을 찾는 것이다. object function을 최대화 시키는 방법은 3가지가 있다.

Finite Difference Policy Gradient

numerical한 방법을 사용한다. 조금씩 값을 바꾸어 보면서 gradient를 구하는 방법이고 하나하나씩 천천히 최적의값을 찾는 방법이다. 매우 비효율적이다. 하지만 미분법을 이용하지 않더라도 동작한다.

\[\frac{\partial J(\theta)}{\partial \theta_k} \approx \frac{J(\theta + \epsilon u_k) - J(\theta))}{\epsilon}\]
  • 각 파라미터를 \(\epsilon\) 만큼 움직여서 k번째 목적함수 \(w,r,t,\theta\)의 계속해서 최적의 값을 찾을때까지 편미분을 측정한다.

Monte Carlo Policy Gradient : REINFORCE 알고리즘

이 방법은 object function의 gradient를 구해서 업데이트 시켜주는 방법이다. gradient descent와 같은 개념이라고 생각하면 될것같다. gradient를 구하는 방법은 아래와 같다.

score function

monte

사용가능한 Policy Example

  • Softmax Policy
\[\pi(s,a) = \frac{e^{\theta^{T}\phi_{sa}}}{\sum_b e^{\theta^{T}\phi_{sb}}}\]
  • Gaussian Policy
\[\pi_{\theta}(s,a) = \frac{1}{\sigma\sqrt{2\pi}}e(-\frac{(a-\mu(s))^2}{2\sigma^2})\]

\(\phi_sa\) : 어떠한 상태에서의 행동의 대한 value값 Q function 개념

policy gradient theorem

output이 바로 보상으로 추출되는 것 말고 Q function을 사용해서 연산할 수 있다.

monte2

REINFORCE

monte carlo policy gradient를 REINFORCE 알고리즘이라고 부른다.

이 알고리즘을 표현하면

  1. \(\theta\)를 초기화한다.
  2. episode를 진행한다. => 게임이 끝난다.
  3. \(\theta\)를 업데이트한다.

monte3

\(v_t\) : 실제 적용되는 reward

개념을 이해하기는 어렵지만 알고리즘은 간단하다.

결론 : policy를 이용해서 object function을 만들고 object function을 최대화하는 \(\theta\)값을 업데이트 해서 찾는다. policy을 이용해서 object function 정의하는 방법과 object function을 최대화 하는 방법을 배웠고 이러한 과정이 최종적으로 policy를 학습하게 한다.

1
2
3
4
5
6
7
8

--> state
--> Network
--> output
--> softmax(output) = action       [policy]
--> reward maximize(loss minimize) [maximize]
--> theta update                   [backpropagation]
--> action                         
--> state`

참조

reinforcement
This post is licensed under CC BY 4.0 by the author.