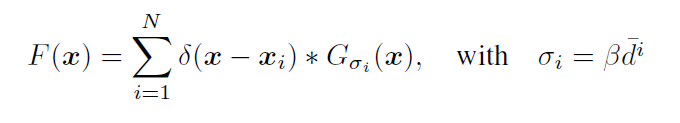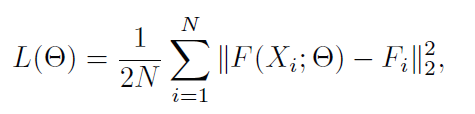MCNN 끄적이기
MCNN
Single-Image Crowd Counting via Multi-Column Convolutional Neural Network [paper]
Dataset
개요
중국 상하이에서 대규모 밀입국 사건으로 35명이 숨졌다. 그 이후로 더 많은 희생자들이 있다고 주장하는 많은 이야기들이 있었다. 이미지와 비디오로부터 인파를 정확하게 추정하는 것은 군중 통제와 공공 안전의 목적으로 컴퓨터 비전 기술의 점점 더 중요한 응용이 되었다.
문제점
대부분의 기존 작업에서는 foreground segmentation이 불가결하다. foreground segmentation은 도전적인 과제이고 부정확한 분할은 최종 계산에 나쁜 영향을 미친다. 따라서 foreground segmentation을 하지않고 인원수를 추정해야한다.
인구의 밀도와 분포는 우리의 작업에 따라 크게 다르고 일반적으로 각 이미지에 있는 대부분의 사람들은 큰 혼란을 발생시킨다. 따라서 전통적인 탐지 기반 방법은 이러한 이미지와 상황에서 잘 동작하지 않는다.
영상에 나타난 인물의 스케일에 큰 변화가 있을 수 있기 때문에, 서로 다른 영상에 대한 군중 수를 정확하게 추정하기 위해, 서로 다른 스케일의 형상을 모두 함께 활용해야 한다.
특징
3개의 컬럼이 서로 다른 크기(대규모,중규모,소규모)의 필터에 대응하여 각 칼럼 CNN이 학습한 특징을 원근효과로 인한 사람/머리크기의 변화에 적응하도록 하기 위함이다.
MCNN에서는 fully connection layer를 필터 크기가 1x1인 convolution layer 로 교체한다. 따라서 모델의 input image는 왜곡을 피하기 위해 임의의 크기가 될 수 있다. 네트워크의 즉각적인 output은 전체 카운터를 도출하는 사람들의 밀도를 추정하는 것이다.
Dataset은 상하이텍이라는 대규모 군중 데이터 세트를 사용한다. 파트A는 인터넷에서 무작위로 가져온 것이고 파트B는 상하이 대도시의 번화가에서 얻은 것이다.
해결방안
CNN을 통해 특정 이미지에 있는 사람의 수를 추정하기 위해서는 네트워크의 입력이 이미지이고 출력은 people count 이다.
Density map은 많은 정보를 보존한다. 예를 들어, 작은 지역의 밀도가 다른 지역의 밀도에 비해 훨씬 높다면, 그것은 그곳에서 비정상적인 일이 발생했다는 것을 나타낼 수 있다.
CNN을 통해 Density map을 학습 할 때, 학습된 필터는 크기가 다른 헤드에 더 잘 적응하므로, 다른 원근 효과를 가진 임의의 입력에 더 적합하다. 그러므로 필터는 좀더 의미심장하며, people count의 정확도를 향상시킨다.
발견
머리 크기 간 밀도 맵의 근본적인 관계를 찾기 어렵다. 흥미롭게도 우리는 머리의 크기가 붐비는 장면에서 두 이웃의 중심 사이의 거리와 관련이 있다는 것을 발견했다. 따라서 이웃에 대한 평균 거리를 바탕으로 각 사람의 확산 매개변수를 데이터 적응적으로 결정할 것을 제안한다.
알고리즘
주어진 이미지에서 각 머리 xi에 대해, 논문은 그것의 가장 가까운 이웃에 대한 거리를 {d1,d2,d3 ‘’’} 로 표현한다. 따라서 xi와 관련된 픽셀은 di에 비례하는 반경에서 지면상의 영역에 해당합니다. 그러므로 di에 비례하는 분산 σi를 갖는 Gaussian kernel로 σ(x-xi)를 컨볼루션 할 필요가 있다. 보다 정확하게 밀도 F는 어떤 파라미터 β에 대한 것이어야 한다. 다시 말하면 지리 정보 적응형 커널이라고 불리는 각 데이터 포인트 주변의 local geometry에 적응할 수 있는 밀도 커널로 label H를 컨볼루션합니다. 결과적으로 β = 0.3이 가장 좋은 결과를 제공한다는 것을 발견 했다.
밀도 추정용 MCNN
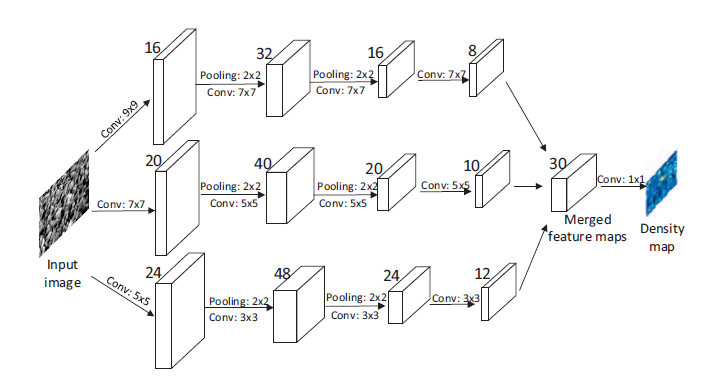
원근 왜곡으로 인해 이미지들은 크기가 매우 다른 머리를 포함하므로, 동일한 크기의 receptive field가 있는 필터는 서로 다른 스케일의 군중 밀도의 특성을 포착할 수 없을 것이다. 그러므로, Density maps의 raw pixel로 부터 map을 학습하기 위해 다른 크기의 local receptive field를 사용하는 것이 더 자연스럽다.
서로 다른 크기의 머리에 대응한 density map을 모델화하기 위해, 서로 다른 크기의 필터를 사용한다.
세개의 병렬 CNN을 포함하고 있다.
각 2x2 필터 영역마다 max pooling 적용
활성화함수 : relu
계산상의 복잡성(최적화 파라미터의 수)를 줄이기 위해, large CNN에 더 적은 filter를 사용한다.
모든 CNN의 출력인 feature map을 쌓아서 density map에 매핑한다. feature map을 density map에 매핑하기 위해 1x1 필터를 사용한다.
Loss
- Θ는 학습 가능한 파라미터의 집합
- N은 훈련 이미지의 수
- xi는 입력 이미지
- Fi는 진짜 density map
- F(xi;Θ)는 샘플 xi로 생성된 추정 density map
- L : 추정 밀도와 진짜 밀도의 손실
최적화
- SGD : stochastic gradient descent
- backpropagation
그러나 실제로는 훈련용 샘플의 수가 매우 제한적이고, dnn에 대한 gradient vanishing 문제가 있기 때문에 배우기 쉽지 않다. RBM의 사전 훈련에 영감을 받아 네 번째 layer에 회선층의 출력을 density map에 직접 매핑함으로써, 각 단열의 CNN을 개별적으로 미리 학습한다. 그런 다음 미리 훈련된 CNN을 사용하여 CNN을 초기화하고 모든 파라미터를 동시에 미세 조정한다.
RBM
- Restricted Boltzmann machine : 제한된 볼츠만 머신
- input layer 와 hidden layer로 구성이 되어있다.
- 입력받은 데이터를 hidden layer에 얼마나 전달할 것인지 확률에 따라 결정 한다.(stochastic decision) 그렇게 만들어진 hidden layer의 출력으로 부터 input을 다시 만들어내고 이런 과정이 반복을 해가면서 hidden layer의 출력과 hidden layer를 찾아 나가는 알고리즘이다.
SGD
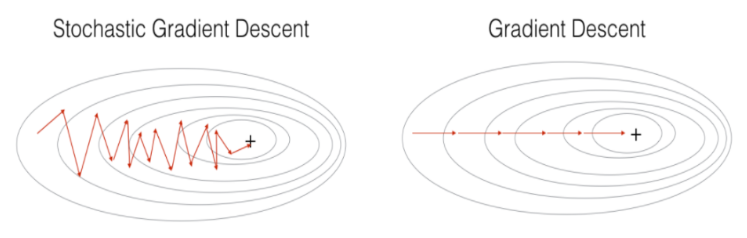
- Stochastic gradient descent : 확률 경사 하강법
- 배치크기가 1인 경사하강법 알고리즘
- 기존 배치가 너무 커지면 중복의 가능성이 높아질수 있다. -> 만약에 훨씬 적은 계산으로 적절한 기울기를 얻을 수 있다면 어떨까?
- 각 배치를 포함하는 하나의 예가 무작위로 선택된다.
단점
- 반복이 충분하면 효과가 있지만 노이즈가 매우 심하다.
- 최저점을 찾지 못할수가 있다.
해결방안 : 미니배치 SGD
- 미니 배치 : 10개에서 1000개 사이의 데이터 배치
- 노이즈를 줄이면서 전체 배치보다는 효과적이다.
전이학습(Transfer learning) 설정
MCNN 모델의 한 가지 이점은 필터들이 크기가 다른 사람의 머리에 density map을 모델링하는 방법을 배운다는 것이다.
- 처음으로 몇 개의 layer를 fix해서 학습한 지식을 보존 할 수 있다.
- 마지막 몇 개의 layer를 미세 조정함으로써 모델을 대상 영역에 적응시킬 수 있다.
결론
- 2016년에 나쁘지 않은 성능을 자랑하고 있다.