DCN 톺아보기

DCN

(Deformable Convolutional Networks)

• DCN Paper : Here
• Official Code : Here

Abstract

Convolutional neural networks (CNNs) are inherently limited to model geometric transformations due to the fixed geometric structures in their building modules.

CNN은 고정적인 기하학적 구조로 인해서 모델의 기하학적 변환이 본질적으로 제한된다.

이 논문에서는 deformable convolution 과 deformable ROI pooling을 제안한다. 두 가지 방법 모두 추가적인 supervision없이 offsets을 학습하고 추가적인 offsets으로 spatial sampling location을 확장한다. 위에 제안한 모듈(deformable)은 일반 모듈(normal)을 쉽게 대체할 수 있고 backpropagation도 쉽게 할 수있다.

object detection과 semantic segmentation과 같은 vision task에 효과적이다.

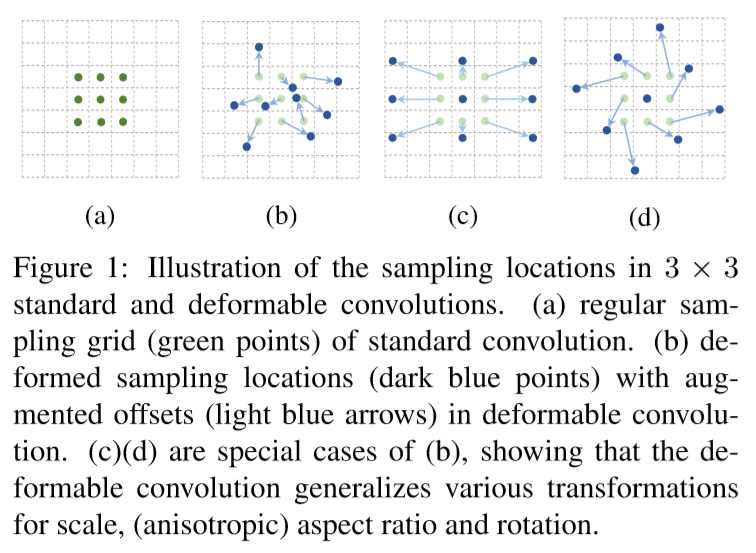
기하학적 변환 : 같은 이미지 내의 object는 여러가지 스케일이나 형태를 가질 수 있다. 이러한 같은 공간(이미지) 내의 형태 변환

Introduction

visual recognition의 주요 과제는 object scale, pos, viewpoint, part deformation에서의 geometric transformations, geometric variations를 적응하는 방법이다.

일반적으로 2가지 방법이 있다.

• 원하는 변형이 충분히 있는 training datasets을 만든다.

이것은 일반적으로 image를 augmentation 하는 방법이 있다. 효과가 좋지만 이미지를 augmentation해서 훈련하는데 시간이 많이들고 설정해야하는 parameter가 많아진다.

• transformation invariant features 과 알고리즘을 사용한다.

SIFT나 sliding window 기반의 object detection과 같은 잘 알려진 기술이 포함된다.

SIFT

• Scale-Invariant Feature Transform
• 이미지의 변화(크기와 회전)에 대해 불변하는 특징을 추출하는 알고리즘

• 매우 복잡한 변화에는 약하다.

---

현재 이미지 처리에 자주 사용되는 CNN은 고정 된 위치에서 feature map을 sampling한다. Pooling은 고정 된 비율로 spatial resolution을 감소시키고, ROI Pooling은 고정 된 spatial bins로 분리한다. 기하학적 변환을 처리하기위한 내부 매커니즘이 없다.

고정 된 위치 말고 서로 다른 위치를 가진다면 여러 scale과 변형을 갖는 object에 대응할 수 있기 때문에, scale과 receptive field 크기를 적응적으로 결정하는 것이 좋다.

그래서 deformable convolution과 deformable ROI Pooling을 소개한다.

먼저 deformable convolution을 살펴보면 offsets은 추가적인 convolution layer를 통해 이전 feature map에서 학습된다. 따라서 deformation은 input feature 에 국부적이고 조밀하며 적응적 방식으로 조절된다.

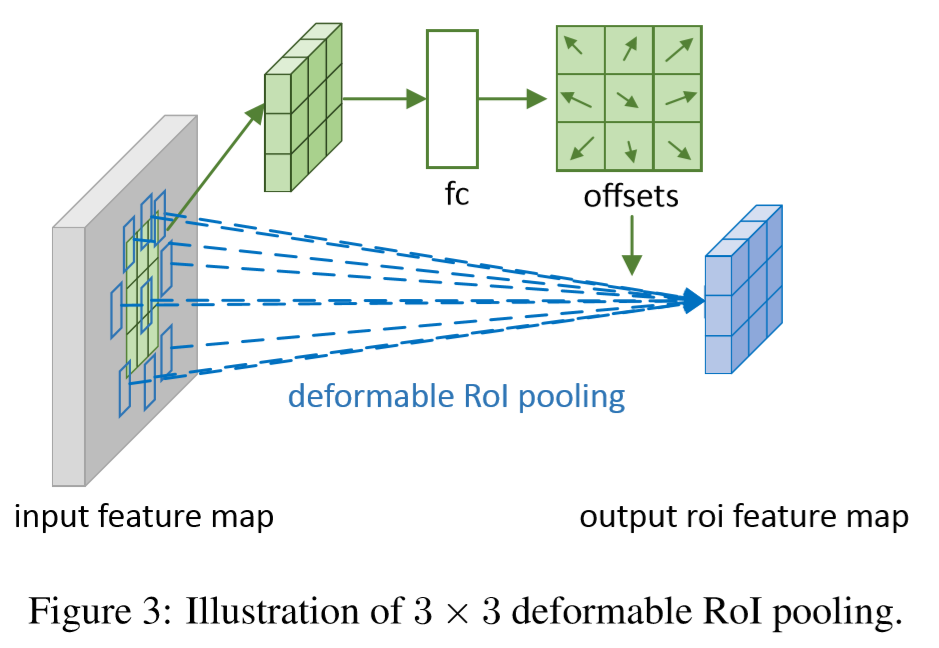
그다음 deformable ROI Pooling은 이전 ROI Pooling에 bin partition에서 각 bin 위치에 offsets을 추가한다. 아래 그림을 보면 이해하기 쉬울 것이다.

Deformable Convolution Networks

2D convolution은 2단계로 구성된다.

1. 입력 feature map x에 대해 정규 그리드 \(R\)을 사용해서 샘플링
2. w에 의해 가중된 샘플링 된 값의 합산, 그리드 \(R\)은 수용 가능한 size 및 dilation을 정의한다. 예를 들어

\[R = \left \{ \left ( -1,-1 \right ), \left ( -1,0 \right ),...,\left ( 0,1 \right ), \left ( 1,1 \right ) \right \}\]

dilation 1, 3x3 kernel로 정의한다.

convolution

\[y(p_0) = \sum_{p_n \in R}w(p_n) \cdot x(p_0 + p_n)\]

• \(p_0\) : output feature map y에서 위치
• \(p_n\)는 \(R\)의 위치값들

deformable convolution

\[y(p_0) = \sum_{p_n \in R}w(p_n) \cdot x(p_0 + p_n + \Delta p_n)\] \[\left \{ \Delta p_n|n=1,...,N \right \}\] \[N=|R|\]

• \(\Delta p_n\) : offsets 일반적으로 분수다. 따라서 위치를 보정하기 위해 위 식은 bilinear interpolation으로 구현된다.

\[x(p) = \sum_q G(q,p) \cdot x(q)\] \[G(q,p) = g(q_x,p_x) \cdot g(q_y,p_y)\] \[g(a,b) = max(0,1-|a - b|)\]

• \(p\) : \(p_0 + p_n + \Delta p_n\)

• \(q\) : feature map x에서 모든 필수적인 공간적 위치를 순회하는 변수라고 한다… 보간법을 위해 사용될 주변 픽셀이라고 생각하면 될것 같다.

• \(G(·,·)\) : bilinear interpolation kernel 이다. 2차원이다. 2개의 1차원 kernel로 분리되어있다.

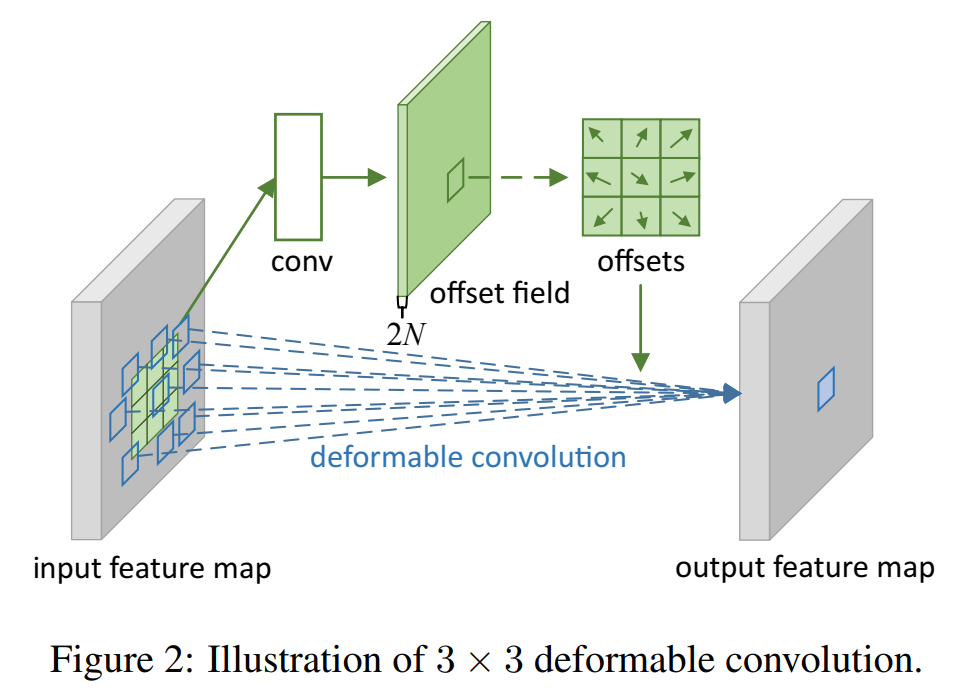
최종적으로 convolution을 위한 kernel을 유동적으로 변하게 하기위해서 offsets field를 학습시킨다.

offsets channel이 2N인 이유는 2D offsets이기 때문이다.

bilinear interpolation kernel

• linear interpolation

\[f(x) = \frac{\left | x - x_2 \right |}{\left | x - x_1 \right | + \left | x - x_2 \right |}f(x_1) + \frac{\left | x - x_1 \right |}{\left | x - x_1 \right | + \left | x - x_2 \right |}f(x_2)\]

수직선 상에 두 점의 값으로 수직선 내 두 점 사이에 값을 알 수 있다.

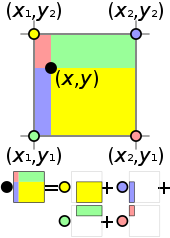
• bilinear interpolation

각 선에 대해서(상,하,좌,우) 선형 보간으로 x값과 y값을 구한다.

---

Deformable ROI Pooling

임의의 크기의 영역을 고정 크기의 feature map으로 변환하는 작업을 한다.

ROI Pooling

k x k개의 bins으로 나누고 k x k의 feature map y를 출력한다.

\[y(i,j) = \sum_{p \in bin(i,j)} x(p_0 + p) / n_{ij}\] \[\left \lfloor i\frac{w}{k} \right \rfloor \leq p_x \leq \left \lceil (i+1)\frac{w}{k} \right \rceil\] \[\left \lfloor j\frac{h}{k} \right \rfloor \leq p_y \leq \left \lceil (j+1)\frac{h}{k} \right \rceil\]

• \(n_{ij}\) : bin안에 있는 pixel의 수

deformable ROI Pooling

\[\Delta p_{ij} = \gamma \cdot \Delta \hat{p_{ij}} ◦ (w, h)\] \[\gamma = 0.1\] \[y(i,j) = \sum_{p \in bin(i,j)} x(p_0 + p + \Delta p_{ij}) / n_{ij}\] \[\left \{ \Delta p_{ij}|0 \leq i,j \leq k \right \}\]

위에 fully connected layer에서 정규화 된 offset \(\Delta \hat{p_{ij}}\)을 생성하고 위에 식으로 \(\Delta p_{ij}\)로 변환시킨다. \(\gamma\)는 offset의 크기를 변경시키기 위해 미리 정의된 스칼라값이다.

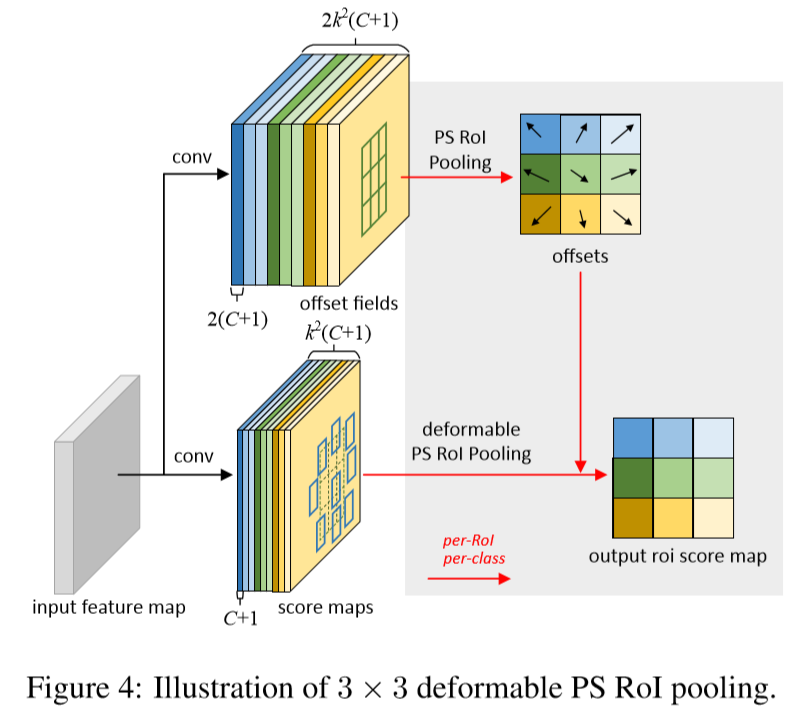
Position-Sensitive(PS) ROI Pooling

fully convolution이고 ROI Pooling과 다르다고 한다. convolution layer를 통해서 모든 input feature map은 각 object class에 대한 \(k^2\) score map(C개의 클래스면 C+1)으로 변환된다. 클래스를 구별 할 필요없이, 이러한 score maps은 \(\left \{ x_{i,j} \right \}\)로 표시되고 여기서 \((i,j)\)는 모든 bins의 수다. 이러한 score maps에서 Pooling이 수행된다. \((i,j)\)번째 bin에 대한 출력값은 그 bin에 대응하는 하나의 score maps \(\left \{ x_{i,j} \right \}\)의 합산으로 얻어진다.

ROI Pooling과 deformable ROI Pooling과 차이점은 일반 feature map이 score map으로 변하는 것이다. 역전파 또한 fully convolution으로 바뀌어서 다르다.

Deformable ConvNets

위에 나온 deformable convolution과 ROI Pooling은 동일한 입출력 크기를 갖는다. 그래서 기존에 있는 모델에 쉽게 적용시킬 수 있다.

offsets 학습을 위한 convolution layer와 fully connected layer는 가중치를 0으로 초기화한다.

1. fully convolution network는 전체 input image에 대해 feature map을 생성한다. - feature extraction model

2. shallow task specific network는 feature map에서 결과를 생성한다. - segmentation and detection model

기존 모델에 추가를 어떻게 했는지에 대한 설명은 논문을 보면서 알면 될것같다.

---

Backpropagation

• deformable convolution

\[\frac{\partial y(p_0)}{\partial \Delta p_n} = \sum_{p_n \in R} w(p_n) \cdot \frac{\partial x(p_0 + p_n + \Delta p_n)}{\partial \Delta p_n} =\] \[= \sum_{p_n \in R} \left [w(p_n) \cdot \sum _q \frac{\partial G(q,p_0 + p_n + \Delta p_n)}{\partial \Delta p_n} x(q) \right ]\]

• deformable ROI Pooling

\[\frac{\partial y(p_0)}{\partial \Delta p_n} = \frac{1}{n_{ij}} \sum_{p_n \in bin(i,j)} \frac{\partial x(p_0 + p_n + \Delta p_n)}{\partial \Delta p_n} =\] \[= \frac{1}{n_{ij}} \sum_{p_n \in bin(i,j)} \left [\sum _q \frac{\partial G(q,p_0 + p_n + \Delta p_n)}{\partial \Delta p_n} x(q) \right ]\]

---

Benchmark